
题目列表(包括答案和解析)
 ”表示).
”表示).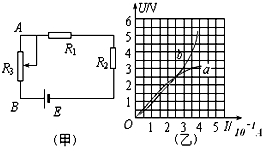
 ”表示).
”表示).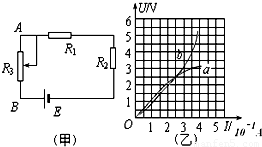
 ”表示).
”表示).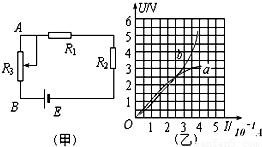
 ”表示).
”表示).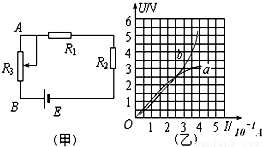
 ”表示).
”表示).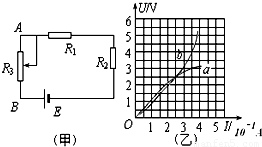
题号
1
2
3
4
5
6
7
8
9
10
答案
D
BD
C
B
AB
AC
A
C
BC
CB
11.(1) (2)BC
D ABCD
(2)BC
D ABCD
12.⑴R1(2分) ⑵电路图如右图所示(4分)(有任何错误不得分)
⑶1.47(2分)(1.46~1.48均给2分)0.83(2分) (0.81~0.85均给2分)
 13.解:(1)设木块相对小车静止时小车的速度为V,
13.解:(1)设木块相对小车静止时小车的速度为V,
根据动量守恒定律有:mv=(m+M)V

(2)对小车,根据动能定理有:


14.解:(1)K接a时,R1被短路,外电阻为R2,根据电功率公式可得
通过电源电流  A
A
电源两端电压 V
V
(2)K接a时,有E=U1+I1r=4+r ①
K接b时,R1和R2串联, R′外=R1+R2=6 Ω
通过电源电流I2= A
A
这时有:E=U2+I2r=4.5+0.75 r ②
解①②式得:E=6 V r=2 Ω
(3)当K接c时,R总=R1+r+R23=6 Ω
总电流I3=E/R总=
通过R2电流I'= I3=
I3=
15.解:(1)0~25 s内一直处于上升阶段,上升的最大高度在数值上等于△OAB的面积, 即H= ×25×
×25×
(2)9 s末发动机关闭,此后探测器只受重力作用,故在这一阶段的加速度即为该行星表面的重力加速度,由图象得
g= =
= m/s2=
m/s2=
(3)由图象知加速上升阶段探测器的加速度:
a= m/s2
m/s2
根据牛顿运动定律,得
F-mg=ma
所以推力F=m(g+a)=1.67×104 N
16.解:(1)带负电粒子射入磁场后,由于受到洛伦兹力的作用,粒子将沿图示的轨迹运动,从A点射出磁场,设O、A间的距离为L,射出时速度的大小仍为v,射出方向与x轴的夹角仍为θ,由洛伦兹力公式和牛顿定律可得:

qv0B=m
式中R为圆轨道半径,解得:
R= ①
①
圆轨道的圆心位于OA的中垂线上,由几何关系可得:
 =Rsinθ ②
=Rsinθ ②
联解①②两式,得:L=
所以粒子离开磁场的位置坐标为(- ,0)
,0)
(2)因为T= =
=
所以粒子在磁场中运动的时间,t=
17.解:由题图得,皮带长s= =
=
(1)工件速度达v0前,做匀加速运动的位移s1= t1=
t1= 
达v0后做匀速运动的位移s-s1=v0(t-t1)
解出加速运动时间 t1=0.8 s
加速运动位移 s1=
所以加速度a= =
=
工件受的支持力N=mgcosθ
从牛顿第二定律,有μN-mgsinθ=ma
解出动摩擦因数μ=
(2)在时间t1内,皮带运动位移s皮=v0t=
在时间t1内,工件相对皮带位移 s相=s皮-s1=
在时间t1内,摩擦发热 Q=μN?s相=60 J
工件获得的动能 Ek= mv02=20 J
mv02=20 J
工件增加的势能Ep=mgh=150 J
电动机多消耗的电能W =Q+Ek十Ep=230 J
18、①由 可求得vm,
可求得vm,
②由 ,解得h,
,解得h,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com