
题目列表(包括答案和解析)
如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连。质量为m、边长为l、电阻不计的正方形线框垂直于导轨并可在导轨上滑动。整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B。滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,绳处于拉直状态。现若从静止开始释放物块,用h表示物块下落的高度(物块不会
触地),g表示重力加速度,其他电阻不计,则 ( )
A.因通过正方形线框的磁通量始终不变,故电阻R中没有感应电流
B.物体下落的加速度为0.5g
C.若h足够大,物体下落的最大速度为![]()
D.通过电阻R的电量为![]()

如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连。质量为m、边长为l、电阻不计的正方形线框垂直于导轨并可在导轨上滑动。整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B。滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,绳处于拉直状态。现若从静止开始释放物块,用h表示物块下落的高度(物块不会触地),g表示重力加速度,其他电阻不计,则 ( )
A.因通过正方形线框的磁通量始终不变,故电阻R中没有感应电流
B.物体下落的加速度为0.5g
C.若h足够大,物体下落的最大速度为![]()
D.通过电阻R的电量为![]()
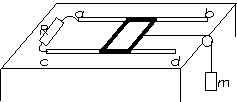
如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连。质量为m、边长为l、电阻不计的正方形线框垂直于导轨并可在导轨上滑动。整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B。滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,绳处于拉直状态。现若从静止开始释放物块,用h表示物块下落的高度(物块不会触地),g表示重力加速度,其他电阻不计,则( )
A.因通过正方形线框的磁通量始终不变,故电阻R中没有感应电流
B.物体下落的加速度为0.5g
C.若h足够大,物体下落的最大速度为![]()
D.通过电阻R的电量为![]()

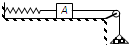 如图所示,木块A放在水平桌面上.木块左端用轻绳与轻质弹簧相连,弹簧的左端固定,用一轻绳跨过光滑定滑轮,一端连接木块右端,另一端连接一砝码盘(装有砝码),轻绳和弹簧都与水平桌面平行.当砝码和砝码盘的总质量为0.5kg时,整个装置静止,弹簧处于伸长状态,弹力大小为3N.若轻轻取走盘中的部分砝码,使砝码和砝码盘的总质量减小到0.1kg,取g=10m/s2,此时装置将会出现的情况是( )
如图所示,木块A放在水平桌面上.木块左端用轻绳与轻质弹簧相连,弹簧的左端固定,用一轻绳跨过光滑定滑轮,一端连接木块右端,另一端连接一砝码盘(装有砝码),轻绳和弹簧都与水平桌面平行.当砝码和砝码盘的总质量为0.5kg时,整个装置静止,弹簧处于伸长状态,弹力大小为3N.若轻轻取走盘中的部分砝码,使砝码和砝码盘的总质量减小到0.1kg,取g=10m/s2,此时装置将会出现的情况是( )| A、弹簧伸长的长度减小 | B、桌面对木块的摩擦力大小不变 | C、木块向右移动 | D、木块所受合力将变大 |
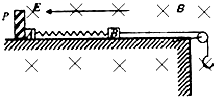 如图所示,光滑绝缘水平桌面上固定一绝缘挡板P,质量分别为mA和mB的小物块A和B(可视为质点)分别带有+QA和+QB的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B连接,另一端连接轻质小钩.整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B、方向水平向里的匀强磁场中.物块A,B开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面.若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则
如图所示,光滑绝缘水平桌面上固定一绝缘挡板P,质量分别为mA和mB的小物块A和B(可视为质点)分别带有+QA和+QB的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B连接,另一端连接轻质小钩.整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B、方向水平向里的匀强磁场中.物块A,B开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面.若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则题号
1
2
3
4
5
6
7
8
9
答案
D
A
C
A
B
BCD
ACD
AC
AC
10、1)0.495~
 (3)
(3) (2分)偏大(2分)因纸带与打点记时器间存在摩擦阻力f,则有
(2分)偏大(2分)因纸带与打点记时器间存在摩擦阻力f,则有 即
即
11、⑴a
⑵a)P
 b)如图
b)如图
⑶
12、(1)

(2)BC (3)速度 频率 (4)全反射 光疏介质 临界角
13、(1)A (2)AD (3)
14【解析】(1)设小物体运动到p点时的速度大小为v,对小物体由a运动到p过程应用动能定理得  ①
①
 ②
s=vt ③
②
s=vt ③
联立①②③式,代入数据解得s=
(2)设在数字“
 ⑤ 联立①⑤式,代入数据解得F=0.3N ⑥ 方向竖直向下
⑤ 联立①⑤式,代入数据解得F=0.3N ⑥ 方向竖直向下
15【解析】⑴做直线运动有: 做圆周运动有:
做圆周运动有:
只有电场时,粒子做类平抛,有:


 解得:
解得:
 粒子速度大小为:
粒子速度大小为:
速度方向与x轴夹角为:
粒子与x轴的距离为:
⑵撤电场加上磁场后,有: 解得:
解得:
粒子运动轨迹如图所示,圆心C位于与速度v方向垂直的直线上,该直线与x轴和y轴的夹角均为π/4,有几何关系得C点坐标为:


过C作x轴的垂线,在ΔCDM中:

解得:
M点横坐标为:
16【解析】
(1)由于列车速度与磁场平移速度方向相同,导致穿过金属框的磁通量发生变化,由于电磁感应,金属框中会产生感应电流,该电流受到安培力即为驱动力。
(2)为使列车获得最大驱动力,MM、PQ应位于磁场中磁感应强度同为最大值且反向的地方,这会使得金属框所围面积的磁通量变化率最大,导致线框中电流最强,也会使得金属框长边中电流收到的安培力最大,因此,d应为 的奇数倍,即
的奇数倍,即
 ①
①
(3)由于满足(2)问条件,则MM、PQ边所在处的磁感应强度大小均为B0且方向总相反,经短暂的时间Δt,磁场沿Ox方向平移的距离为v0Δt,同时,金属框沿Ox方向移动的距离为vΔt。
因为v0>v,所以在Δt时间内MN边扫过磁场的面积S=(v0-v)lΔt
在此Δt时间内,MN边左侧穿过S的磁通量移进金属框而引起框内磁通量变化
ΔΦMN = B
同理,该Δt时间内,PQ边左侧移出金属框的磁通引起框内磁通量变化
ΔΦPQ
= B
故在Δt内金属框所围面积的磁通量变化 ΔΦ = ΔΦMN +ΔΦPQ④
根据法拉第电磁感应定律,金属框中的感应电动势大小 ⑤
⑤
根据闭合电路欧姆定律有 ⑥
⑥
根据安培力公式,MN边所受的安培力FMN = B0Il
PQ边所受的安培力FPQ = B0Il
根据左手定则,MM、PQ边所受的安培力方向相同,此时列车驱动力的大小
F = FMN + FPQ = 2 B0Il⑦
联立解得 ⑧
⑧
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com