
题目列表(包括答案和解析)
已知复数![]() ,
,![]() ,其中
,其中![]() ,
,![]() 为虚数单位.
为虚数单位.
(1)若![]() 是实数(其中
是实数(其中![]() 为
为![]() 的共轭复数),求实数
的共轭复数),求实数![]() 的值;
的值;
(2)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
已知复数![]() ,
,![]() ,其中
,其中![]() ,
,![]() 为虚数单位.
为虚数单位.
(1)若![]() 是实数(其中
是实数(其中![]() 为
为![]() 的共轭复数),求实数
的共轭复数),求实数![]() 的值;
的值;
(2)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
已知复数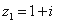 ,
,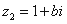 ,
,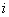 为虚数单位,若
为虚数单位,若 为纯虚数,则实数
为纯虚数,则实数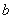 的值是
的值是
已知复数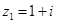 ,
, ,
,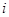 为虚数单位,若
为虚数单位,若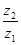 为纯虚数,则实数
为纯虚数,则实数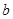 的值是
的值是
已知复数 ,
, ,
, 为虚数单位,若
为虚数单位,若 为纯虚数,则实数
为纯虚数,则实数 的值是
的值是
1.2 2.有的素数不是奇数 3. 4.0 5.
4.0 5.
6. 7.
7. 8.[0,2] 9.
8.[0,2] 9. 10.-3 11.-1
10.-3 11.-1
12.④ 13. 14.①③
14.①③
15.解:(1)因为 ,所以
,所以 ,
,
即 
而  ,所以
,所以 .故
.故 
(2)因为 
所以  .
.
由 得
得  所以
所以 
从而 故
故 的取值范围是
的取值范围是 .
.
16.(1)证明:因为PB^平面ABCD,MA^平面ABCD,
所以PB∥MA.
因PBÌ平面BPC,MA (/平面BPC,
所以MA∥平面BPC.同理DA∥平面BPC,
因为MAÌ平面AMD,ADÌ平面AMD,
MA∩AD=A,所以平面AMD∥平面BPC.
(2)连接AC,设AC∩BD=E,取PD中点F,
连接EF,MF.
因ABCD为正方形,所以E为BD中点.
因为F为PD中点,所以EF∥=PB.
因为AM∥=PB,所以AM∥=EF.所以AEFM为平行四边形.所以MF∥AE.
因为PB^平面ABCD,AEÌ平面ABCD,所以PB^AE.所以MF^PB.
因为ABCD为正方形,所以AC^BD.
所以MF^BD.所以MF^平面PBD.又MFÌ平面PMD.
所以平面PMD^平面PBD.
17.解:(1) 令
令
则
由于 ,则
,则 在
在 内的单调递增区间为
内的单调递增区间为 和
和
(2)依题意, 由周期性
由周期性 

(3)函数 为单调增函数,且当
为单调增函数,且当 时,
时, ,
,
此时有
当 时,由于
时,由于 ,而
,而 ,则有
,则有 ,
,
即 ,即
,即
而函数 的最大值为
的最大值为 ,且
,且 为单调增函数,
为单调增函数,
则当 时,恒有
时,恒有 ,
,
综上,在 内恒有
内恒有 ,所以方程
,所以方程 在
在 内没有实数解.
内没有实数解.
18.解:(1)由题意得:(100-x)? 3000 ?(1+2x%) ≥100×3000,
即x2-50x≤0,解得0≤x≤50, 又∵x>0 ∴0<x≤50;
(2)设这100万农民的人均年收入为y元,
则y= =
即y=-[x-25(a+1)]2+3000+475(a+1)2 (0<x≤50)
(i)当0<25(a+1)≤50,即0<a≤1,当x=25(a+1)时,y最大;
(ii)当25(a+1)>50,即a >1,函数y在(0,50]单调递增,∴当x=50时,y取最大值.
答:在0<a≤1时,安排25(a+1)万人进入企业工作,在a>1时安排50万人进入企业
工作,才能使这100万人的人均年收入最大.
19.(1)解:由①知: ;由③知:
;由③知: ,即
,即 ; ∴
; ∴
(2 ) 证明:由题设知: ;
;
由 知
知 ,得
,得 ,有
,有 ;
;
设 ,则
,则 ,
, ;
;
∴
即 ∴函数
∴函数 在区间[0,1]上同时适合①②③.
在区间[0,1]上同时适合①②③.
(3) 证明:若 ,则由题设知:
,则由题设知: ,且由①知
,且由①知 ,
,
∴由题设及③知:
 ,矛盾;
,矛盾;
若 ,则则由题设知:
,则则由题设知: , 且由①知
, 且由①知 ,
,
∴同理得:
 ,
,
矛盾;故由上述知:  .
.
20.解: (1) 由题设知: 对定义域中的
对定义域中的 均成立.
均成立.
∴ .
.
即 ∴
∴ 对定义域中的
对定义域中的 均成立.
均成立.
∴ 即
即 (舍去)或
(舍去)或 . ∴
. ∴  .
.
(2) 由(1)及题设知: ,
,
设 ,
,
∴当 时,
时, ∴
∴ .
.
当 时,
时, ,即
,即 .
.
∴当 时,
时, 在
在 上是减函数.
上是减函数.
同理当 时,
时, 在
在 上是增函数.
上是增函数.
(3) 由题设知:函数 的定义域为
的定义域为 ,
,
∴①当 时,有
时,有 . 由(1)及(2)题设知:
. 由(1)及(2)题设知: 在
在 为增函数,由其值域为
为增函数,由其值域为 知
知 (无解);
(无解);
②当 时,有
时,有 .由(1)及(2)题设知:
.由(1)及(2)题设知: 在
在 为减函数, 由其值域为
为减函数, 由其值域为 知
知 得
得 ,
, .
.
(4) 由(1)及题设知:
 ,
,
则函数 的对称轴
的对称轴 ,
,
 ∴
∴ .
.
∴函数 在
在 上单调减.
上单调减.
∴

 是最大实数使得
是最大实数使得 恒有
恒有 成立,
成立,

∴ ,即
,即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com