（本题14分）有两个不透明的箱子，每个箱子都装有个完全相同的小球，球上分别标有数字。

甲从其中一个箱子中摸出一个球，乙从另一个箱子摸出一个球，谁摸出的球上标的数字大谁就获胜（若数字相同则为平局），求甲获胜的概率；

摸球方法与（1）同，若规定：两人摸到的球上所标数字相同甲获胜，所标数字不相同则乙获胜，这样规定公平吗？请说明理由。

（本题满分14分）某班同学利用春节进行社会实践，对本地岁的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，将生活习惯符合低碳观念

   的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图。

人数统计表：               （二）各年龄段人数频率分布直方图：

（Ⅰ）在答题卡给定的坐标系中补全频率分布直方图，并求出、、的值；

（Ⅱ）从岁年龄段的“低碳族”中采用分层抽样法抽取人参加户外低碳体验活

     动。若将这个人通过抽签分成甲、乙两组，每组的人数相同，求岁中被

     抽取的人恰好又分在同一组的概率；

（Ⅲ）根据所得各年龄段人数频率分布直方图，估计在本地岁的人群中“低碳

      族”年龄的中位数。

(本小题满分14分)

       小明参加一次智力问答比赛，比赛共设三关。第一、二关各有两个问题，两个问题全答对，可进入下一关。第三关有三个问题，只要答对其中两个问题，则闯关成功。每过一关可一次性获得价值分别为100、300、500元的奖励。小明对三关中每个问题回答正确的概率依次为、、，且每个问题回答正确与否相互独立。

   （1）求小明过第一关但未过第二关的概率；

   （2）用表示小明所获得奖品的价值，求的分布列和期望。

（本小题满分14分）

某商场“十.一”期间举行有奖促销活动,顾客只要在商店购物满８00元就能得到一次摸奖机会.摸奖规则是:在盒子内预先放有5个相同的球,其中一个球标号是０，两个球标号都是４０，还有两个球没有标号。顾客依次从盒子里摸球，每次摸一个球（不放回），若累计摸到两个没有标号的球就停止摸球，否则将盒子内球摸完才停止.奖金数为摸出球的标号之和（单位：元），已知某顾客得到一次摸奖机会。

（1）求该顾客摸三次球被停止的概率；

（2）设（元）为该顾客摸球停止时所得的奖金数，求的分布列及数学期望.

（本小题满分14分）

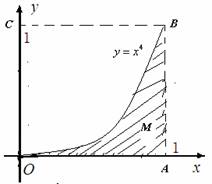Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分，这时等于由曲线，轴，所围成的区域M的面积，为求它的值，我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷个点，若个点中有个点落入中，则的面积的估计值为，此即为定积分的估计值I。向正方形中随机投掷10000个点，有个点落入区域M

(1)若=2099，计算I的值，并以实际值比较误差是否在5%以内

(2)求的数学期望

(3)用以上方法求定积分，求I与实际值之差在区间（—0.01,0.01）的概率

附表：