
题目列表(包括答案和解析)
(本小题满分12分)
已知函数
(Ⅰ)若曲线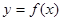 在
在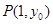 处的切线平行于直线
处的切线平行于直线 ,求函数
,求函数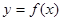 的单调区间;
的单调区间;
(Ⅱ)若函数 在
在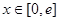 上有两个零点,求实数
上有两个零点,求实数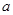 的取值范围。
的取值范围。
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分,作答时请在答题纸上所选题目题号的方框内打“√”。
(本小题满分12分)
已知函数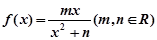 在
在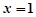 处取到极值2
处取到极值2
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)设函数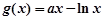 .若对任意的
.若对任意的 ,总存在唯一的
,总存在唯一的 ,使得
,使得 ,求实数
,求实数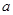 的取值范围.
的取值范围.
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分12分)
已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(I)求a,b的值;
(II)如果当x>0,且![]() 时,
时,![]() ,求k的取值范围.
,求k的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑.
(本小题满分12分)
已知点![]() ,过点
,过点![]() 作抛物线
作抛物线![]()
![]() 的切线
的切线![]() ,切点
,切点![]() 在第二象限,如图.
在第二象限,如图.
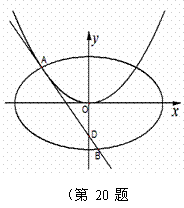 (Ⅰ)求切点
(Ⅰ)求切点![]() 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为![]() 的椭圆
的椭圆![]() 恰好经过切点
恰好经过切点![]() ,设切线
,设切线![]() 交椭圆的另一点为
交椭圆的另一点为![]() ,记切线
,记切线![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() ,求椭圆方程.
,求椭圆方程.
21(本小题满分12分)
已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:![]()
![]() .
.
22.选修4-1:几何证明选讲
如图,![]() 是圆
是圆![]() 的直径,
的直径,![]() 是弦,
是弦,![]() 的平分线
的平分线![]() 交圆
交圆![]() 于点
于点![]() ,
,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() 。
。
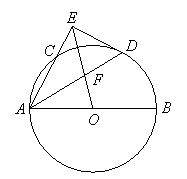 (1)求证:
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值。
的值。
23.选修4—4:坐标系与参数方程
在平面直角坐标系中,直线![]() 过点
过点![]() 且倾斜角为
且倾斜角为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点;
两点;
(1)若![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的取值范围;
的取值范围;
(2)求弦![]() 最短时直线
最短时直线![]() 的参数方程。
的参数方程。
24. 选修4-5 不等式选讲
已知函数![]()
(I)试求![]() 的值域;
的值域;
(II)设![]() ,若对
,若对![]() ,恒有
,恒有![]() 成立,试求实数a的取值范围。
成立,试求实数a的取值范围。
(本小题满分12分)
已知函数![]() ,
,![]() 且
且![]() .
.
(Ⅰ)求![]() 的定义域;
的定义域;
(Ⅱ)判断![]() 的奇偶性并予以证明;
的奇偶性并予以证明;
(Ⅲ)当![]() 时,求使
时,求使![]() 的
的![]() 的取值范围.
的取值范围.
(22)(本小题满分12分)
已知![]() 为圆
为圆![]() 上任一点,且点
上任一点,且点![]() .
.
(Ⅰ)若![]() 在圆
在圆![]() 上,求线段
上,求线段![]() 的长及直线
的长及直线![]() 的斜率;
的斜率;
(Ⅱ)求![]() 的最大值和最小值.
的最大值和最小值.
2009年曲靖一种高考冲刺卷理科数学(一)
一、
1 B
10B
1依题意得.files/image252.gif) ,所以
,所以.files/image254.gif) 故
故.files/image256.gif) ,因此选B
,因此选B
2依题意得.files/image258.gif) 。又
。又.files/image260.gif) 在第二象限,所以
在第二象限,所以.files/image262.gif) ,
,
.files/image264.gif) ,故选C
,故选C
3 .files/image266.gif)
且.files/image268.gif) ,
,
.files/image270.gif) 因此选A
因此选A
4 由.files/image272.gif)
因为.files/image274.gif) 为纯虚数的充要条件为
为纯虚数的充要条件为.files/image276.gif)
故选A
5如图,.files/image278.gif)
.files/image282.gif)
.files/image284.gif) 故选A
故选A
6.设.files/image286.gif)
则.files/image288.gif)
.files/image290.gif) 故选D
故选D
7.设等差数列.files/image292.gif) 的首项为
的首项为.files/image294.gif) ,公差
,公差.files/image296.gif) ,因为
,因为.files/image060.gif) 成等比数列,所以
成等比数列,所以.files/image299.gif) ,即
,即.files/image301.gif) ,解得
,解得.files/image303.gif) ,故选D
,故选D
8.由.files/image305.gif) ,所以
,所以.files/image307.gif) 分
分.files/image309.gif) 之比为2,设
之比为2,设.files/image068.gif) (
(.files/image312.gif) ,
,.files/image314.gif) 则
则.files/image316.gif) ,又点
,又点.files/image318.gif) 在圆
在圆.files/image066.gif) 上,所以
上,所以.files/image321.gif) ,即
,即.files/image323.gif) +
+.files/image325.gif) -4,化简得
-4,化简得.files/image327.gif) =16,故选C
=16,故选C
9.长方体的中心即为球心,设球半径为.files/image329.gif) ,则
,则
.files/image331.gif)
.files/image333.gif)
.files/image335.gif) 于是
于是.files/image084.gif) 两点的球面距离为
两点的球面距离为.files/image338.gif) 故选B
故选B
10.先分别在同一坐标系上画出函数.files/image340.gif) 与
与.files/image342.gif) 的图象(如图1)
的图象(如图1)
.files/image343.jpg)
.files/image344.jpg)
观察图2,显然,选B
.files/image133.jpg) 11.依题意,
11.依题意,.files/image346.gif)
.files/image133.jpg)
.files/image348.gif) 故
故.files/image350.gif)
.files/image133.jpg)
.files/image352.gif) 故选C
故选C
.files/image133.jpg) 12.由题意知,
12.由题意知,
.files/image133.jpg)
.files/image354.gif)
.files/image356.gif) ①
①
.files/image133.jpg)
.files/image358.gif) 代入式①得
代入式①得
.files/image133.jpg)
.files/image360.gif)
.files/image133.jpg)
.files/image362.gif)
.files/image133.jpg) 由方程
由方程.files/image121.gif) 的两根为
的两根为.files/image365.gif)
.files/image133.jpg)
.files/image367.gif) 又
又.files/image369.gif)
.files/image133.jpg)
.files/image371.gif) 即
即.files/image373.gif) 故选A。
故选A。
二、
13.5 14.7 15.22 16.①
13.5.线性规划问题先作出可行域,注意本题已是最优的特定参数的特点,可考虑特殊的交点,再验证,由题设可知
.files/image375.gif) 应用运动变化的观点验证满足
应用运动变化的观点验证满足.files/image377.gif) 为所求。
为所求。
14.7. 由题意得.files/image379.gif) 又
又.files/image381.gif)
因此A是钝角,.files/image383.gif)
15.22,连接.files/image385.gif)
.files/image387.gif) ,
,.files/image389.gif)
.files/image391.gif) 的周章为
的周章为.files/image393.gif)
16.①当.files/image395.gif) 时,
时,.files/image397.gif) ,取到最小值,因次,
,取到最小值,因次,.files/image395.gif) 是对称轴:②当
是对称轴:②当.files/image400.gif) 时,
时,.files/image402.gif) 因此
因此.files/image169.gif) 不是对称中心;③由
不是对称中心;③由.files/image405.gif) ,令
,令.files/image407.gif) 可得
可得.files/image409.gif) 故
故.files/image171.gif) 在
在.files/image412.gif) 上不是增函数;把函数
上不是增函数;把函数.files/image414.gif) 的图象向左平移
的图象向左平移.files/image177.gif) 得到
得到.files/image417.gif)
.files/image419.gif) 的图象,得不到
的图象,得不到.files/image171.gif) 的图象,故真命题序号是①。
的图象,故真命题序号是①。
三
17.(1).files/image422.gif) 在
在.files/image424.gif) 上单调递增,
上单调递增,
.files/image426.gif) 在
在.files/image424.gif) 上恒成立,即
上恒成立,即.files/image429.gif) 在
在.files/image424.gif) 上恒成立,
上恒成立,.files/image432.gif) 即实数
即实数.files/image014.gif) 的取值范围
的取值范围.files/image435.gif)
(2).files/image437.gif)
.files/image439.gif) 由题设条件知
由题设条件知.files/image171.gif) 在
在.files/image442.gif) 上单调递增。
上单调递增。
由.files/image444.gif) 得
得.files/image446.gif) ,即
,即.files/image448.gif)
.files/image450.gif)
.files/image452.gif)
.files/image454.gif)
.files/image456.gif)
即.files/image444.gif) 的解集为
的解集为.files/image459.gif)
又.files/image461.gif)
.files/image463.gif)
.files/image444.gif) 的解集为
的解集为.files/image466.gif)
18.(1)过.files/image468.gif) 作
作.files/image470.gif) 子
子.files/image472.gif) 连接
连接.files/image474.gif)
.files/image476.gif) 侧面
侧面.files/image478.gif)
.files/image480.gif) 。
。.files/image481.jpg)
.files/image483.gif)
.files/image485.gif) 故
故.files/image487.gif) 是边长为2的等边三角形。又
是边长为2的等边三角形。又.files/image489.gif) 点,
点,.files/image491.gif) 又
又.files/image493.gif) 是
是.files/image495.gif) 在底面
在底面.files/image193.gif) 上的射影,
上的射影,.files/image498.gif)
(法一)(2).files/image500.gif)
.files/image502.gif) 就是二面角
就是二面角.files/image201.gif) 的平面角,
的平面角,.files/image505.gif) 和
和.files/image507.gif) 都是边长为2的正三角形,
都是边长为2的正三角形,.files/image509.gif) 又
又.files/image511.gif)
.files/image513.gif) 即二面角
即二面角.files/image201.gif) 的大小为45°
的大小为45°
(3)取.files/image495.gif) 的中点为
的中点为.files/image517.gif) 连接
连接.files/image519.gif) 又
又.files/image521.gif) 为
为.files/image523.gif) 的中点,
的中点,.files/image525.gif) ,又
,又.files/image527.gif) ,且
,且.files/image529.gif) 在平面
在平面.files/image531.gif) 上,又
上,又.files/image533.gif) 为
为.files/image495.gif) 的中点,
的中点,.files/image536.gif) 又
又.files/image538.gif)
.files/image540.gif)
.files/image542.gif) 线段
线段.files/image229.gif) 的长就是
的长就是.files/image468.gif) 到平面
到平面.files/image203.gif) 的距离在等腰直角三角形
的距离在等腰直角三角形.files/image547.gif) 中,
中,.files/image549.gif) ,
,.files/image551.gif) ,
,.files/image553.gif) ,即
,即.files/image468.gif) 到平面
到平面.files/image203.gif) 的距离是
的距离是.files/image557.gif)
(法二)(2).files/image559.gif) ,
,.files/image542.gif) 以
以.files/image562.gif) 为
为.files/image274.gif) 轴、
轴、.files/image565.gif) 轴、
轴、.files/image567.gif) 轴建立空间直角坐标系,则点
轴建立空间直角坐标系,则点.files/image569.gif)
.files/image571.gif) 设平面
设平面.files/image573.gif) 的法向量为
的法向量为.files/image575.gif) ,则
,则.files/image577.gif) ,解得
,解得.files/image109.gif) ,
,.files/image580.gif) 取
取.files/image582.gif) 则
则.files/image584.gif) ,平面
,平面.files/image193.gif) 的法向量
的法向量.files/image587.gif)
.files/image589.gif)
.files/image542.gif) 向量
向量.files/image592.gif) 所成角为45°故二面角
所成角为45°故二面角.files/image201.gif) 的大小为45°,
的大小为45°,
(3)由.files/image595.gif) ,
,.files/image597.gif) 的中点
的中点.files/image599.gif) 设平面
设平面.files/image203.gif) 的法向量为
的法向量为.files/image602.gif) ,则
,则.files/image604.gif) ,解得
,解得.files/image606.gif) 则
则.files/image608.gif) 故
故.files/image468.gif) 到平面
到平面.files/image203.gif) 的距离为
的距离为.files/image612.gif)
19.(1).files/image614.gif) 取值为0,1,2,3,4
取值为0,1,2,3,4
.files/image616.gif)
.files/image618.gif) 的分布列为
的分布列为
.files/image614.gif)
0
1
2
3
4
P
.files/image621.gif)
.files/image623.gif)
.files/image625.gif)
.files/image627.gif)
.files/image629.gif)
.files/image631.gif) (2)由
(2)由.files/image633.gif)
即.files/image635.gif)
又.files/image637.gif)
所以,当.files/image639.gif) 时,由
时,由.files/image641.gif) 得
得.files/image643.gif)
当.files/image645.gif) 时,由
时,由.files/image647.gif) 得
得.files/image649.gif)
.files/image651.gif) 即为所求‘
即为所求‘
20.(1).files/image653.gif) 在一次函数
在一次函数.files/image214.gif) 的图像上,
的图像上,
.files/image656.gif)
于是.files/image658.gif) ,且
,且.files/image660.gif)
.files/image542.gif) 数列
数列.files/image219.gif) 是以
是以.files/image664.gif) 为首项,公比为2的等比数列
为首项,公比为2的等比数列
(3)
由(1)知.files/image666.gif)
21.(1)由题意得:
.files/image668.gif)
.files/image669.jpg)
.files/image542.gif) 点Q在以M、N为焦点的椭圆上,即
点Q在以M、N为焦点的椭圆上,即.files/image672.gif)
.files/image542.gif) 点Q的轨迹方程为
点Q的轨迹方程为.files/image674.gif)
(2).files/image676.gif)
.files/image678.gif)
.files/image680.gif)
设点O到直线AB的距离为.files/image682.gif) ,则
,则.files/image684.gif)
.files/image686.gif)
当.files/image688.gif) 时,等号成立
时,等号成立
.files/image542.gif) 当
当.files/image688.gif) 时,面积的最大值为3
时,面积的最大值为3
22.(1)
.files/image691.gif)
(2)由题意知
.files/image693.gif)
(3)等价证明.files/image695.gif)
由(1)知
.files/image697.gif)
.files/image699.gif)
.files/image701.gif)
.files/image703.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com