
题目列表(包括答案和解析)
已知函数![]() 满足
满足![]() ,且
,且![]()
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)设![]() ,
,![]() ,求证:
,求证:![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
(3)设![]() ,对每一个
,对每一个![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数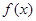 满足对任意实数
满足对任意实数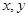 都有
都有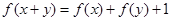 成立,且当
成立,且当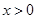 时,
时,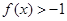 ,
,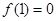 .
.
(1)求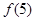 的值;
的值;
(2)判断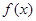 在
在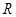 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数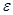 ,总能找到一个正实数
,总能找到一个正实数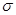 ,使得当
,使得当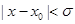 时,
时,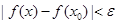 ,则称函数
,则称函数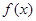 在
在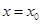 处连续。试证明:
处连续。试证明: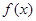 在
在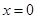 处连续.
处连续.
已知函数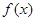 满足对任意实数
满足对任意实数 都有
都有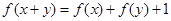 成立,且当
成立,且当 时,
时,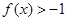 ,
, .
.
(1)求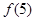 的值;
的值;
(2)判断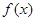 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数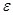 ,总能找到一个正实数
,总能找到一个正实数 ,使得当
,使得当 时,
时,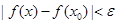 ,则称函数
,则称函数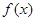 在
在 处连续。试证明:
处连续。试证明: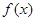 在
在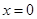 处连续.
处连续.
| 1 |
| 2 |
| x-y |
| 1-xy |
| 1 |
| 2 |
| 2an | ||
1+
|
| 1 |
| f(a1) |
| 1 |
| f(a2) |
| 1 |
| f(an) |
| m-8 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
一、选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.C 2.C 3.C 4.C 5.A 6.D 7.A 8.A 9.B
10.D 11.A 12.B
二、填空题:本大题4共小题,每小题5分。
13..files/image334.gif) 14.
14..files/image336.gif) 15.
15..files/image338.gif) 16.①④
16.①④
三、解答题(解答应写出文字说明,证明过程或演算步骤)
17.(I).files/image340.gif)
.files/image342.gif)
.files/image343.jpg) 由余弦定理得
由余弦定理得.files/image345.gif)
整理得得.files/image347.gif) 。
。
.files/image349.gif) ,故
,故.files/image138.gif) 为直角三角形
为直角三角形
(Ⅱ)设.files/image138.gif) 内角
内角.files/image353.gif) 对边的边长分别是
对边的边长分别是.files/image355.gif)
.files/image357.gif) 外接圆半径为1,
外接圆半径为1,.files/image359.gif)
.files/image361.gif)
.files/image363.gif)
.files/image365.gif) 周长的取值范围
周长的取值范围.files/image367.gif)
18.(I)证明:.files/image369.gif) ,
,
.files/image371.gif)
(Ⅱ)解:设.files/image373.gif) A
A
.files/image375.jpg)
.files/image377.gif)
设点.files/image216.gif) 到平面
到平面.files/image218.gif) 的距离为
的距离为.files/image381.gif) ,
,
.files/image383.gif)
(Ⅲ解:设.files/image385.gif) 轴建立空间直角坐标宿,为计算方便,不妨设
轴建立空间直角坐标宿,为计算方便,不妨设.files/image387.gif)
.files/image389.gif)
.files/image391.gif)
.files/image393.gif)
.files/image394.jpg) 要使二面角
要使二面角.files/image222.gif) 的大小为120°,则
的大小为120°,则.files/image397.gif)
即当.files/image399.gif) 时,二面角
时,二面角.files/image222.gif) 的大小为120°
的大小为120°
19.(I)记“厂家任意取出4件产品检验,其中至少有一件是合格品“为事件A,
则.files/image402.gif)
(Ⅱ).files/image404.gif) 的可能取值为0,1,2,
的可能取值为0,1,2,
.files/image406.gif)
所以.files/image404.gif) 的概率分布为
的概率分布为
.files/image404.gif)
0
1
2
.files/image251.gif)
.files/image411.gif)
.files/image413.gif)
.files/image415.gif)
.files/image417.gif)
20.(I)设.files/image419.gif)
.files/image421.gif)
(Ⅱ)曲线.files/image239.gif) 向左平移1一个单位,得到曲线
向左平移1一个单位,得到曲线.files/image242.gif) 的方程为
的方程为.files/image425.gif)
(1)当.files/image427.gif)
(2)当.files/image429.gif)
.files/image431.gif)
(Ⅲ).files/image433.gif)
.files/image435.gif)
21.(I).files/image437.gif)
.files/image439.gif)
(Ⅱ)令.files/image441.gif) ,
,
.files/image443.gif)
(Ⅲ)用数学归纳法证明
.files/image445.gif)
.files/image447.gif)
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分,做答时,用2B铅笔在答题卡上把所选题目对应的题号涂黑。
22..files/image449.gif)
.files/image451.gif)
23.(I).files/image453.gif) (
(.files/image315.gif) 为参数,
为参数,.files/image317.gif) 为倾斜角,且
为倾斜角,且.files/image319.gif) )
)
.files/image458.gif)
(Ⅱ).files/image460.gif)
.files/image462.gif)
24..files/image464.gif)
.files/image466.gif)
.files/image468.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com