王老师给同学们布置了这样一道习题：一个数的算术平方根为2m-6，它的平方根为±（m-2），求这个数．小张的解法如下：依题意可知，2m-6是m-2或者是-（m-2）两数中的一个，（1）
当2m-6=m-2，解得m=4．　（2）
所以这个数为（2m-6）=（2×4-6）=4．　（3）
当2m-6=-（m-2）时，解得m=．（4）
所以这个数为（2m-6）=（2×-6）=y（4x²-4xy+y²）． （5）
综上可得，这个数为4或（a²+4）（a+2）（a-2）．（6）
王老师看后说，小张的解法是错误的．你知道小张错在哪里吗？为什么？请予改正．

王老师给同学们布置了这样一道习题：一个数的算术平方根为2m - 6，它的平方根为±（m - 2），求这个数。小张的解法如下：依题意可知，2m - 6是m - 2或者是-（m - 2）两数中的一个， （1）

当2m - 6 = m - 2，解得m = 4。  （2）

所以这个数为（2m - 6）=（2×4 - 6）= 4。  （3）

当2m – 6 = -（m - 2）时，解得m =  。（4）

所以这个数为（2m - 6）=（2×- 6）=  。 （5）

综上可得，这个数为4或  。（6）

王老师看后说，小张的解法是错误的。你知道小张错在哪里吗？为什么？请予改正。

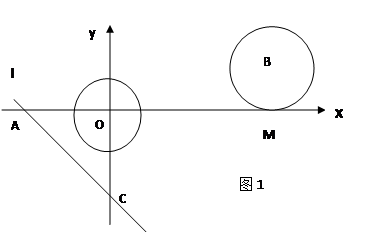
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为－1,直线l y=－X－与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M. 

(1)  求点A的坐标及∠CAO的度数;       

(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?

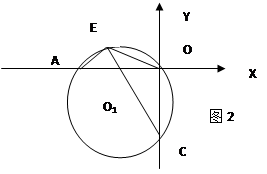
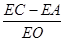(3)如图2.过A,O,C三点作⊙O₁,点E是劣弧上一点,连接EC,EA.EO,当点E在劣弧上运动时(不与A,O两点重合),的值是否发生变化?如果不变,求其值,如果变化,说明理由.                                                    

.                       

【解析】（1）已知点A，C的坐标，故可推出OA=OC，最后可得∠CAO=45°．

（2）依题意，设⊙B平移t秒到⊙B₁处与⊙O第一次相切，连接B₁O，B₁N，则MN=3．连接B₁A，B₁P可推出∠PAB₁=∠NAB₁．又因为OA=OB₁=，故∠AB₁O=∠NAB₁，∠PAB₁=∠AB₁O继而推出PA∥B₁O．然后在Rt△NOB₁中∠B₁ON=45°，∴∠PAN=45°得出∠1=90°．然后可得直线AC绕点A平均每秒30度．

（3）在CE上截取CK=EA，连接OK，证明△OAE≌△OCK推出OE=OK，∠EOA=∠KOC，∠EOK=∠AOC=90°．最后可证明