
题目列表(包括答案和解析)
A、
| ||
B、
| ||
C、
| ||
| D、无法判断 |
 28、如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.
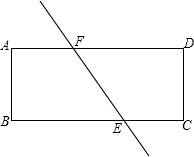
28、如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.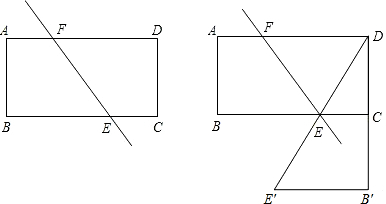 接后,下方梯形记作EE′B′C.当x:n为何值时,直线E′E经过原矩形的顶点D.
接后,下方梯形记作EE′B′C.当x:n为何值时,直线E′E经过原矩形的顶点D.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com