
题目列表(包括答案和解析)
设椭圆![]() 的焦点分别为
的焦点分别为![]() 、
、![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)试求椭圆的方程;
(2)过![]() 、
、![]() 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于![]() 、
、![]() 、
、![]() 、
、![]() 四点(如图所示),试求四边形
四点(如图所示),试求四边形![]() 面积的最大值和最小值.
面积的最大值和最小值.
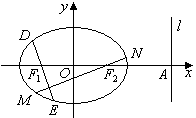
设椭圆 的焦点分别为
的焦点分别为 、
、 ,直线
,直线 :
: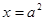 交
交 轴于点
轴于点 ,且
,且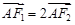 .
.
(1)试求椭圆的方程;
(2)过 、
、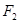 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于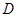 、
、 、
、 、
、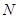 四点(如图所示),试求四边形
四点(如图所示),试求四边形 面积的最大值和最小值.
面积的最大值和最小值.
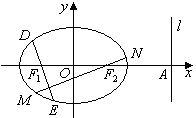
 的焦点分别为
的焦点分别为 、
、 ,直线
,直线 :
: 交
交 轴于点
轴于点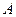 ,且
,且 .
.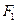 、
、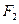 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于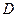 、
、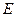 、
、 、
、 四点(如图所示),试求四边形
四点(如图所示),试求四边形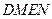 面积的最大值和最小值.
面积的最大值和最小值.
设椭圆![]() 的焦点在
的焦点在![]() 轴上
轴上
(Ⅰ)若椭圆![]() 的焦距为1,求椭圆
的焦距为1,求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,![]() 为椭圆
为椭圆![]() 上的第一象限内的点,直线
上的第一象限内的点,直线![]() 交
交![]() 轴与点
轴与点![]() ,并且
,并且![]() ,证明:当
,证明:当![]() 变化时,点
变化时,点![]() 在某定直线上。
在某定直线上。
设椭圆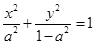 的焦点在
的焦点在 轴上
轴上
(Ⅰ)若椭圆 的焦距为1,求椭圆
的焦距为1,求椭圆 的方程;
的方程;
(Ⅱ)设 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 为椭圆
为椭圆 上第一象限内的点,直线
上第一象限内的点,直线 交
交 轴与点
轴与点 ,并且
,并且 ,证明:当
,证明:当 变化时,点
变化时,点 在某定直线上.
在某定直线上.
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
A
D
C
B
D
C
A
D
B
A
1.答案:D
2.答案:B 由试卷.files/image267.gif)
由试卷.files/image269.gif) ,
,
则,试卷.files/image271.gif)
3.答案:A 由试卷.files/image273.gif) .另该题也可直接用
.另该题也可直接用试卷.files/image019.gif) 的周期
的周期
性解答.
4.答案:D
5.答案:C 由垂直、平行可得.
6.答案:B 由试卷.files/image276.gif) ,
,
试卷.files/image278.gif) ∥
∥试卷.files/image280.gif) ,
,
故试卷.files/image282.gif)
7.答案:D
8.答案:C 试卷.files/image284.gif) 所以:
所以:
试卷.files/image286.gif)
9.答案:D 试卷.files/image288.gif)
10.答案:D 试卷.files/image290.gif) ,
,
题中试卷.files/image292.gif)
故试卷.files/image294.gif)
11.答案:B 试卷.files/image296.gif)
注意到双曲线的对称性可知:试卷.files/image298.gif)
所以试卷.files/image300.gif) .
.
12.答案:A 由于试卷.files/image302.gif)
试卷.files/image304.gif)
试卷.files/image306.gif) ,
,
试卷.files/image308.gif)
试卷.files/image310.gif)
二、填空题:本大题共4小题,每小题5分,共20分.
13.答案:70由图可知:底部周长小于110cm的株树为:
试卷.files/image312.jpg)
试卷.files/image314.gif)
14.答案:10 准线x=-1,试卷.files/image316.gif) ,
,
试卷.files/image318.gif)
15.答案:试卷.files/image320.gif) 如图所示:
如图所示:
试卷.files/image322.gif)
16.答案:从第二行起,周期为8得对应的指头是大拇指.
三、解答题:本大题共5小题,共60分.解答应写出文字说明,证明过程或演算步骤.
17.(本题12分) 解:①设公差为试卷.files/image324.gif) ,公比为
,公比为试卷.files/image326.gif)
试卷.files/image328.gif)
试卷.files/image330.gif)
试卷.files/image332.gif)
试卷.files/image334.gif) …………………………………(6分)
…………………………………(6分)
②试卷.files/image336.gif)
试卷.files/image338.gif)
试卷.files/image340.gif) …………………………………(12分)
…………………………………(12分)
18.(本题12分)
解法一:(1)设试卷.files/image342.gif) 与
与试卷.files/image344.gif) 相交于点P,连接PD,则P为
相交于点P,连接PD,则P为试卷.files/image342.gif) 中点,
中点,
试卷.files/image346.gif)
试卷.files/image328.gif) D为AC中点,
D为AC中点,试卷.files/image332.gif) PD//
PD//试卷.files/image350.gif) 。
。
又试卷.files/image328.gif) PD
PD试卷.files/image352.gif) 平面
平面试卷.files/image344.gif) D,
D,
试卷.files/image332.gif)
试卷.files/image350.gif) //平面
//平面试卷.files/image344.gif) D ……………………(4分)
D ……………………(4分)
(2)试卷.files/image328.gif) 正三棱住
正三棱住试卷.files/image354.gif) ,
,
试卷.files/image332.gif)
试卷.files/image356.gif)
试卷.files/image358.gif) 底面ABC。
底面ABC。
又试卷.files/image328.gif) BD
BD试卷.files/image358.gif) AC
AC
试卷.files/image332.gif)
试卷.files/image361.gif)
试卷.files/image358.gif) BD
BD
试卷.files/image332.gif)
试卷.files/image363.gif) 就是二面角
就是二面角试卷.files/image176.gif) 的平面角。
的平面角。
试卷.files/image328.gif)
试卷.files/image356.gif) =
=试卷.files/image365.gif) ,AD=
,AD=试卷.files/image367.gif) AC=1
AC=1
试卷.files/image332.gif) tan
tan 试卷.files/image363.gif) =
=试卷.files/image369.gif)
试卷.files/image332.gif)
试卷.files/image363.gif) =
=试卷.files/image078.gif) ,
即二面角
,
即二面角试卷.files/image176.gif) 的大小是
的大小是试卷.files/image078.gif) …………………(8分)
…………………(8分)
(3)由(2)作AM试卷.files/image358.gif)
试卷.files/image361.gif) ,M为垂足。
,M为垂足。
试卷.files/image328.gif) BD
BD试卷.files/image358.gif) AC,平面
AC,平面试卷.files/image374.gif)
试卷.files/image358.gif) 平面ABC,平面
平面ABC,平面试卷.files/image374.gif)
试卷.files/image377.gif) 平面ABC=AC
平面ABC=AC
试卷.files/image332.gif) BD
BD试卷.files/image358.gif) 平面
平面试卷.files/image374.gif) ,
,
试卷.files/image328.gif) AM
AM试卷.files/image352.gif) 平面
平面试卷.files/image374.gif) ,
,
试卷.files/image332.gif) BD
BD试卷.files/image358.gif) AM
AM
试卷.files/image328.gif)
试卷.files/image361.gif)
试卷.files/image377.gif) BD = D
BD = D
试卷.files/image332.gif) AM
AM试卷.files/image358.gif) 平面
平面试卷.files/image380.gif) ,连接MP,则
,连接MP,则试卷.files/image382.gif) 就是直线
就是直线试卷.files/image344.gif) 与平面
与平面试卷.files/image344.gif) D所成的角。
D所成的角。
试卷.files/image328.gif)
试卷.files/image356.gif) =
=试卷.files/image365.gif) ,AD=1,
,AD=1,试卷.files/image332.gif) 在Rt
在Rt试卷.files/image385.gif)
试卷.files/image356.gif) D中,
D中,试卷.files/image363.gif) =
=试卷.files/image078.gif) ,
,
试卷.files/image332.gif)
试卷.files/image387.gif) ,
,试卷.files/image389.gif) 。
。
试卷.files/image332.gif)
试卷.files/image391.gif)
试卷.files/image332.gif) 直线
直线试卷.files/image342.gif) 与平面
与平面试卷.files/image344.gif) D所成的角的正弦值为
D所成的角的正弦值为试卷.files/image393.gif) …………………(12分)
…………………(12分)
解法二:
(1)同解法一
(2)如图建立空间直角坐标系,
则D(0,0,0),A(1,0,0),试卷.files/image395.gif) (1,0,
(1,0,试卷.files/image365.gif) ),B(0,
),B(0,试卷.files/image365.gif) ,0),
,0),试卷.files/image399.gif) (0,
(0,试卷.files/image365.gif) ,
,试卷.files/image365.gif) )
)
试卷.files/image332.gif)
试卷.files/image402.gif) =(-1,
=(-1,试卷.files/image365.gif) ,-
,-试卷.files/image365.gif) ),
),试卷.files/image404.gif) =(-1,0,-
=(-1,0,-试卷.files/image365.gif) )
)
试卷.files/image407.gif) 设平面
设平面试卷.files/image174.gif) 的法向量为n=(x,y,z)
的法向量为n=(x,y,z)
则n试卷.files/image409.gif)
n试卷.files/image411.gif)
则有试卷.files/image413.gif) ,得n=(
,得n=(试卷.files/image415.gif) ,0,1)
,0,1)
由题意,知试卷.files/image417.gif) =(0,0,
=(0,0,试卷.files/image365.gif) )是平面
)是平面
ABD的一个法向量。
设n与试卷.files/image419.gif) 所成角为
所成角为试卷.files/image249.gif) ,
,
则试卷.files/image422.gif) ,
,
试卷.files/image332.gif)
试卷.files/image424.gif)
试卷.files/image332.gif) 二面角
二面角试卷.files/image176.gif) 的大小是
的大小是试卷.files/image078.gif)
(3)由已知,得试卷.files/image426.gif) =(-1,
=(-1,试卷.files/image365.gif) ,
,试卷.files/image365.gif) ),n=(
),n=(试卷.files/image415.gif) ,0,1)
,0,1)
则试卷.files/image428.gif)
试卷.files/image332.gif) 直线
直线试卷.files/image342.gif) 与平面
与平面试卷.files/image344.gif) D所成的角的正弦值为
D所成的角的正弦值为试卷.files/image393.gif)
试卷.files/image430.gif)
19.(本题12分)
(1)试卷.files/image432.gif)
因为每人从两种食品中各取一件,两件恰好都是不合格食品的概率为0.02,所以三人分别从中各取一件,恰好有一人取到两件都是不合格品的事件,可看做三次独立重复试验问题。
试卷.files/image434.gif) …………………………………(6分)
…………………………………(6分)
(2)试卷.files/image436.gif)
试卷.files/image438.gif)
试卷.files/image440.gif)
所试卷.files/image184.gif) 求的分布列为:
求的分布列为:
试卷.files/image184.gif)
0
1
2
P
0.72
0.26
0.02
E试卷.files/image184.gif) =
=试卷.files/image443.gif) …………………………(12分)
…………………………(12分)
试卷.files/image202.jpg) 20.(本题12分)
20.(本题12分)
解:(1)由题意,试卷.files/image445.gif)
试卷.files/image447.gif)
试卷.files/image449.gif) 为
为试卷.files/image451.gif) 的中点
的中点
试卷.files/image453.gif)
即:椭圆方程为试卷.files/image455.gif) …………………(5分)
…………………(5分)
(2)方法一:当直线试卷.files/image457.gif) 与
与试卷.files/image196.gif) 轴垂直时,
轴垂直时,试卷.files/image460.gif) ,此时
,此时试卷.files/image462.gif) ,四边形
,四边形试卷.files/image216.gif) 的面积
的面积试卷.files/image464.gif) .同理当
.同理当试卷.files/image466.gif) 与
与试卷.files/image196.gif) 轴垂直时,也有四边形
轴垂直时,也有四边形试卷.files/image216.gif) 的面积
的面积试卷.files/image468.gif) . 当直线
. 当直线试卷.files/image469.gif) ,
,试卷.files/image470.gif) 均与
均与试卷.files/image196.gif) 轴不垂直时,设
轴不垂直时,设试卷.files/image471.gif) :
:试卷.files/image473.gif) ,代入消去
,代入消去试卷.files/image475.gif) 得:
得:试卷.files/image477.gif) 设
设试卷.files/image479.gif) 所以,
所以,试卷.files/image481.gif) , 所以,
, 所以,试卷.files/image483.gif) ,同理
,同理试卷.files/image485.gif) 所以四边形的面积
所以四边形的面积试卷.files/image487.gif)
试卷.files/image489.gif) 令
令试卷.files/image491.gif) 因为
因为试卷.files/image493.gif) 当
当试卷.files/image495.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com