
题目列表(包括答案和解析)
小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的:

①作点A关于直线l的对称点A′.
②连结A′B,交直线l于点P.
则点P为所求.

请你参考小明的作法解决下列问题:
(1)如图,在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使得△PDE的周长最小.

①在图1中作出点P.(三角板、刻度尺作图,保留作图
痕迹,不写作法)
②请直接写出△PDE周长的最小值 .
(2)如图在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺作图,保留作图痕迹,不写作法),并直接写出四边形CGEF周长的最小值 .


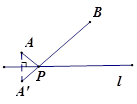


小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的:
①作点A关于直线l的对称点A′.
②连结A′B,交直线l于点P.
则点P为所求.
请你参考小明的作法解决下列问题:
(1)如图,在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使得△PDE的周长最小.
①在图1中作出点P.(三角板、刻度尺作图,保留作图
痕迹,不写作法)
②请直接写出△PDE周长的最小值 .
(2)如图在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺作图,保留作图痕迹,不写作法),并直接写出四边形CGEF周长的最小值 . 
小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的:

①作点A关于直线l的对称点A′.
②连结A′B,交直线l于点P.
则点P为所求.

请你参考小明的作法解决下列问题:
(1)如图,在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使得△PDE的周长最小.

①在图1中作出点P.(三角板、刻度尺作图,保留作图
痕迹,不写作法)
②请直接写出△PDE周长的最小值 .
(2)如图在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺作图,保留作图痕迹,不写作法),并直接写出四边形CGEF周长的最小值 .





湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com