
题目列表(包括答案和解析)

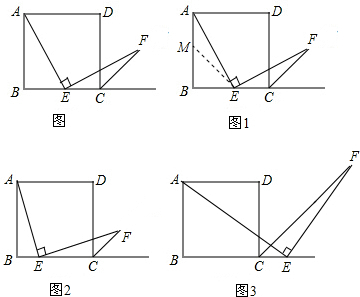
平面内两条直线![]() ∥
∥![]() ,它们之间的距离等于
,它们之间的距离等于![]() .一块正方形纸板
.一块正方形纸板![]() 的边长也等
的边长也等
于![]() .现将这块硬纸板如图所示放在两条平行线上.
.现将这块硬纸板如图所示放在两条平行线上.
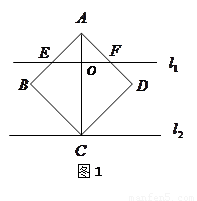
1.如图1,将点C放置在直线![]() 上, 且
上, 且![]() 于O, 使得直线
于O, 使得直线![]() 与
与![]() 、
、![]() 相交于E、F,证明:
相交于E、F,证明:![]() 的周长等于
的周长等于![]() ;
;
2.请你继续完成下面的探索:如图2,若绕点C转动正方形硬纸板![]() ,使得直线
,使得直线![]() 与
与![]() 、
、![]() 相交于E、F,
相交于E、F,
试问![]() 的周长等于
的周长等于![]() 还成立吗?并证明你的结论;
还成立吗?并证明你的结论;
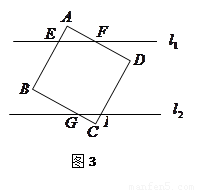
3.如图3,将正方形硬纸片![]() 任意放置,使得直线
任意放置,使得直线![]() 与
与![]() 、
、![]() 相交于E、F,直线
相交于E、F,直线![]() 与
与![]() 、CD相交于G,H,设
、CD相交于G,H,设![]() AEF的周长为
AEF的周长为![]() ,
,![]() CGH的周长为
CGH的周长为![]() ,试问
,试问![]()
![]() ,
,![]() 和
和![]() 之间存在着什么关系?试证明你的结论.
之间存在着什么关系?试证明你的结论.



平面内两条直线 ∥
∥ ,它们之间的距离等于
,它们之间的距离等于 .一块正方形纸板
.一块正方形纸板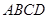 的边长也等
的边长也等
于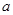 .现将这块硬纸板如图所示放在两条平行线上.
.现将这块硬纸板如图所示放在两条平行线上.
1.如图1,将点C放置在直线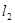 上, 且
上, 且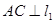 于O, 使得直线
于O, 使得直线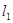 与
与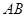 、
、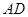 相交于E、F,证明:
相交于E、F,证明: 的周长等于
的周长等于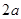 ;
;
2.请你继续完成下面的探索:如图2,若绕点C转动正方形硬纸板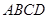 ,使得直线
,使得直线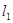 与
与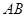 、
、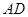 相交于E、F,
相交于E、F,
试问 的周长等于
的周长等于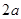 还成立吗?并证明你的结论;
还成立吗?并证明你的结论;
3.如图3,将正方形硬纸片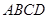 任意放置,使得直线
任意放置,使得直线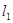 与
与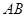 、
、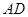 相交于E、F,直线
相交于E、F,直线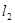 与
与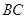 、CD相交于G,H,设
、CD相交于G,H,设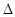 AEF的周长为
AEF的周长为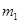 ,
,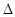 CGH的周长为
CGH的周长为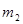 ,试问
,试问
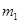 ,
,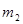 和
和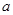 之间存在着什么关系?试证明你的结论.
之间存在着什么关系?试证明你的结论.
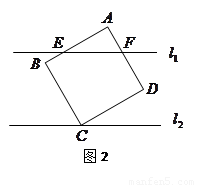
 ∥
∥ ,它们之间的距离等于
,它们之间的距离等于 .一块正方形纸板
.一块正方形纸板 的边长也等
的边长也等 .现将这块硬纸板如图所示放在两条平行线上.
.现将这块硬纸板如图所示放在两条平行线上. 上, 且
上, 且 于O, 使得直线
于O, 使得直线 与
与 、
、 相交于E、F,证明:
相交于E、F,证明: 的周长等于
的周长等于 ;
; ,使得直线
,使得直线 与
与 、
、 相交于E、F,
相交于E、F, 的周长等于
的周长等于 还成立吗?并证明你的结论;
还成立吗?并证明你的结论; 任意放置,使得直线
任意放置,使得直线 与
与 、
、 相交于E、F,直线
相交于E、F,直线 与
与 、CD相交于G,H,设
、CD相交于G,H,设 AEF的周长为
AEF的周长为 ,
, CGH的周长为
CGH的周长为 ,试问
,试问
 ,
, 和
和 之间存在着什么关系?试证明你的结论.
之间存在着什么关系?试证明你的结论.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com