
题目列表(包括答案和解析)
| 3 |
 |
| BC |
| CK |
| PQ |
 .
.
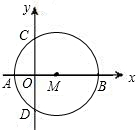
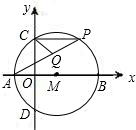
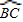 上的一个动点,CQ平分∠PCD.当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变,请求出其变化范围;
上的一个动点,CQ平分∠PCD.当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变,请求出其变化范围;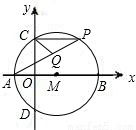
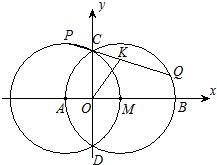
 的值不变;②线段OK的长度不变.其中有且只有一个结论正确,选择正确的结论证明并求其值.
的值不变;②线段OK的长度不变.其中有且只有一个结论正确,选择正确的结论证明并求其值.
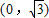 .
.
 上的一个动点,CQ平分∠PCD.当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变,请求出其变化范围;
上的一个动点,CQ平分∠PCD.当P点运动时,线段AQ的长度是否改变?若不变,请求其值;若改变,请求出其变化范围;
 的值不变;②线段OK的长度不变.其中有且只有一个结论正确,选择正确的结论证明并求其值.
的值不变;②线段OK的长度不变.其中有且只有一个结论正确,选择正确的结论证明并求其值.
| 3 |

 |
| BC |

| CK |
| PQ |

张华与李明在讨论问题:“已知线段a、b,求作Rt△ABC,使∠C=90°,AB=a,AC=b”时,提出了如下的画法:1、画线段AB=a;2、以AB为直径画⊙O;3、以A为圆心,b为半径画圆与⊙O交于点C,连接BC,则△ABC为所求作的三角形.

问题1:在张华的画法中,他应用了什么知识得到∠C=90°的?
答:
问题2:已知△ABC中,∠ACB=90°,AC=BC=2,P、Q分别是边AB、BC上的动点,且点P不与A、B重合,点Q不与B、C重合,当CQ的长取不同的值时,
△CPQ是否可能为直角三角形?若可能,请求出CQ的范围;若不能,说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com