（2011广西崇左，21，10分）（本小题满分10分）目前我市“校园手机”现象越来越受到社会的关注.针对这种现象，市辖区某中学班主任李老师在“统计实习”活动中随机调查了学校若干名家长对“中学生带手机到学校”现象的看法，统计整理并制作了如下的统计图：

（1）求这次调查的家长总数及家长表示“无所谓”的人数，并补全图①；

（2）求图②中表示家长“无所谓”的圆心角的度数；

（3）从这次接受调查的家长中，随机抽查一个，恰好是“不赞成”态度的家长的概率是多少？

（2011广西崇左，22，10分）（本小题满分10分）矩形、菱形、正方形都是平行四边形，但它们都是有特殊条件的平行四边形，正方形不仅是特殊的矩形，也是特殊的菱形.因此，我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题：

（1）将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.

（2）要证明一个四边形是正方形，可先证明四边形是矩形，再证明这个矩形的_______相等；或者先证明四边形是菱形，在证明这个菱形有一个角是________ .

（3）某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a²，对此结论，你认为是否正确？若正确，请说明理由；若不正确，请举出一个反例说明.

（本小题满分10分）

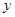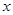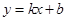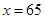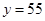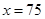某商场试销一种成本为每件60元的服装，经试销发现，销售量（件）与销售单价（元）符合一次函数，且时，；时，．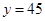

（1）求一次函数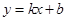的表达式；

（2）若该商场获得利润为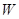元，试写出利润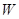与销售单价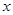之间的关系式；

（3）若该商场想获得500元的利润且尽可能地扩大销售量，则销售单价应定为多少元？

（4）销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？

（本小题满分10分）
某工厂计划为震区生产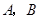两种型号的学生桌椅500套，以解决1250名学生的学习问题，一套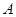型桌椅（一桌两椅）需木料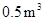，一套型桌椅（一桌三椅）需木料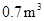，工厂现有库存木料．
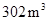【小题1】（1）有多少种生产方案？
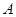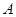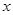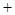【小题2】（2）现要把生产的全部桌椅运往震区，已知每套型桌椅的生产成本为100元，运费2元；每套型桌椅的生产成本为120元，运费4元，求总费用（元）与生产型桌椅（套）之间的关系式，并确定总费用最少的方案和最少的总费用．（总费用生产成本运费）
【小题3】（3）按（2）的方案计算，有没有剩余木料？如果有，请直接写出用剩余木料再生产以上两种型号的桌椅，最多还可以为多少名学生提供桌椅；如果没有，请说明理由．

（本小题满分10分）如图1，点C将线段AB分成两部分，如果AB : AC=AC : BC，那么称点C为线段的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线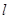将一个面积为S的图形分成两部分，这两部分的面积分别为S₁: S₂，如果S : S₁= S₁: S₂，，那么称直线为该图形的黄金分割线．

（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？

（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？

（3）研究小组探究发现：在（1）中，过点C任作AE交AB于E，再过点D作，交 AC于点F，连接EF（如图3），则直线EF是△ABC的黄金分割线．请说明理由．

（4）如图4，点E是ABCD的边AB的黄金分割点，过点E作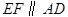，交DC于点F，显然直线EF是ABCD的黄金分割线．请你再画一条ABCD的黄金分割线，使它不经过ABCD各边黄金分割点（保留必要的辅助线）．