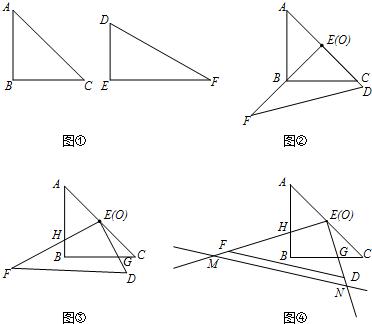
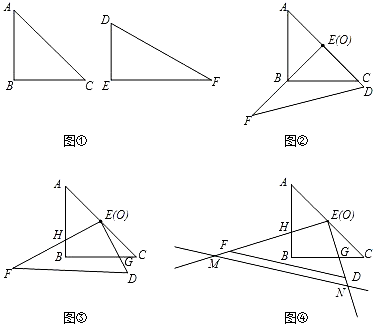
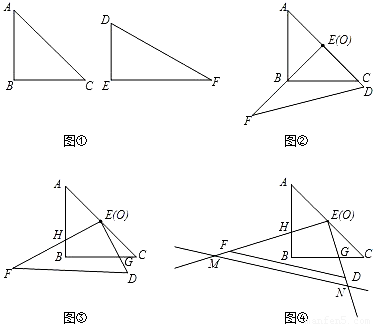
如图①是一副三角板,其中∠B=∠E=90°,∠A=∠C=45°,∠F=30°,AC=EF=2.把两个三角板ABC和DEF叠放在一起(如图②),且使三角板DEF的直角顶点E与三角板ABC的斜边中点O重合,DE和OC重合.现将三角板DEF绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形BGEH是旋转过程中两三角板的重叠部分(如图③).
(1)当旋转角度为45°时,EG和AB之间的数量关系为______.
(2)当DF经过三角板ABC的顶点B,求旋转角α的度数.
(3)在三角板DEF绕O点旋转的过程中,在DF上是否存在一点P,使得∠APC=90°,若存在,请利用直尺和圆规在DF上画出这个点,并说明理由,若不存在,请说明理由.
(4)在射线EF上取一点M,过M作DF的平行线交射线ED于点N(如图④),若直线MN上始终存在两个点P、Q,使得∠APC=∠AQC=90°,求EM的取值范围.

 将一副三角板的直角重合放置,如图1所示,
将一副三角板的直角重合放置,如图1所示,