
题目列表(包括答案和解析)
(本题满分12分)如图1,△ABC的边BC在直线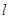 上,AC⊥BC,且AC=BC;△EFP的边FP也在直线
上,AC⊥BC,且AC=BC;△EFP的边FP也在直线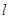 上,边EF与边AC重合,且EF=FP.
上,边EF与边AC重合,且EF=FP.
【小题1】(1)将△EFP沿直线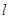 向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
【小题2】(2)将△EFP沿 直线
直线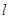 向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连
向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连 结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
【小题3】(3)若AC=BC=4,设△EFP平移的距离为x,当0≤x≤8时,△EFP与△ABC重叠部分的面积为S,请写出S与x之间的函数关系式,并求出最大值.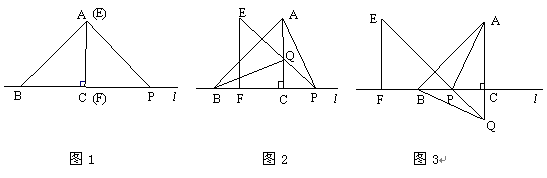
( 本题满分12分)
【小题1】(1)动手操作:
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。
【小题2】(2)观察发现小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由
(3)实践与运用:
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小。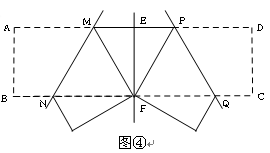
(本小题满分12分)
如图,⊙O的半径为6cm,射线PM与⊙O相切于点C,且PC=16cm.
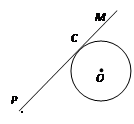
(1)请你作出图中线段PC的垂直平分线EF,垂足为Q,并求出QO的长;
(2)在(1)的基础上画出射线QO,分别交⊙O于点A、B,将直线EF沿射线QM方向以5cm/s的速度平移(平移过程中直线EF始终保持与PM垂直),设平移时间为t.当t为何值时,直线EF与⊙O相切?
(3)直接写出t为何值时,直线EF与⊙O无公共点?t为何值时,
|

|
(本小题满分12分)
如图,⊙O的半径为6cm,射线PM与⊙O相切于点C,且PC=16cm.

(1)请你作出图中线段PC的垂直平分线EF,垂足为Q,并求出QO的长;
(2)在(1)的基础上画出射线QO,分别交⊙O于点A、B,将直线EF沿射线QM方向以5cm/s 的速度平移(平移过程中直线EF始终保持与PM垂直),设平移时间为t.当t为何值时,直线EF与⊙O相切?
(3)直接写出t为何值时,直线EF与⊙O无公共点?t为何值时,
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com