已知二次函数y＝ax²＋bx＋c的图象的顶点坐标为(0，)，且ac＝．

(1)若该函数的图象经过点(－1，－1)．

①求使y＜0成立的x的取值范围．

②若圆心在该函数的图象上的圆与x轴、y轴都相切，求圆心的坐标．

(2)经过A(0，p)的直线与该函数的图象相交于M，N两点，过M，N作x轴的垂线，垂足分别为M₁，N₁，设△MAM₁，△AM₁N₁，△ANN₁的面积分别为s₁，s₂，s₃，是否存在m，使得对任意实数p≠0都有s₂²＝ms₁s₃成立，若存在，求出m的值，若不存在，请说明理由．

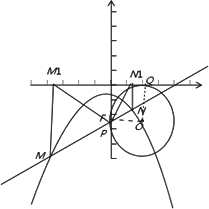
如图，二次函数y＝－ax²＋ax＋a(a＞0)的图象与y轴交于点A，与x轴交于点B、C，过A点作x轴的平行线交抛物线于另一点D，线段OC上有一动点P，连结DP，作PE⊥DP，交y轴于点E．

(1)当a变化时，线段AD的长是否变化？若变化，请说明理由；若不变，请求出AD的长．

(2)若a为定值，设OP＝x，OE＝y，试求y关于x的函数关系式．

(3)若在线段OC上存在不同的两点P₁、P₂使相应的点E₁、E₂都与点A重合，试求a的取值范围．

如图，二次函数y＝ax²的图象与一次函数y＝x＋b的图象相交于A(－2，2)、B两点，从点A和点B分别引平行于y轴的直线与x轴分别交于C，D两点，点P(t，0)，为线段CD上的动点，过点P且平行于y轴的直线与抛物线和直线分别交于R，S．

(1)求一次函数和二次函数的解析式，并求出点B的坐标．

(2)当SR＝2RP时，计算线段SR的长．

(3)若线段BD上有一动点Q且其纵坐标为t＋3，问是否存在t的值，使S_△BRQ＝15．若存在，求t的值；若不存在，说明理由．

在平面直角坐标系xOy中，已知二次函数y＝ax²＋bx＋c(a≠0)的图象与x轴交于A，B两点(点A在点B的左边)，与y轴交于点C，其顶点的横坐标为1，且过点(2，3)和(－3，－12)．

(1)求此二次函数的表达式；

(2)若直线l：y＝kx(k≠0)与线段BC交于点D(不与点B，C重合)，则是否存在这样的直线l，使得以B，O，D为顶点的三角形与△BAC相似？若存在，求出该直线的函数表达式及点D的坐标；若不存在，请说明理由；

(3)若点P是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角∠PCO与∠ACO的大小(不必证明)，并写出此时点P的横坐标x_p的取值范围．