
题目列表(包括答案和解析)
在研究某新措施对“非典”的防治效果问题时,得到如下列联表:
| | 存活数 | 死亡数 | 合计 |
| 新措施 | 132 | 18 | 150 |
| 对照 | 114 | 36 | 150 |
| 合计 | 246 | 54 | 300 |
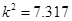 ,故我们由此认为 “新措施对防治非典有效” 的把握为( )
,故我们由此认为 “新措施对防治非典有效” 的把握为( ) C.
C.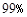 D.
D.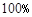
在研究某新措施对“非典”的防治效果问题时,得到如下列联表:
|
|
存活数 |
死亡数 |
合计 |
|
新措施 |
132 |
18 |
150 |
|
对照 |
114 |
36 |
150 |
|
合计 |
246 |
54 |
300 |
由表中数据可得 ,故我们由此认为
“新措施对防治非典有效” 的把握为( )
,故我们由此认为
“新措施对防治非典有效” 的把握为( )
A.0
B. C.
C.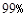 D.
D.
在研究某新措施对“非典”的防治效果问题时,得到如下列联表:
|
|
存活数 |
死亡数 |
合计 |
|
新措施 |
132 |
18 |
150 |
|
对照 |
114 |
36 |
150 |
|
合计 |
246 |
54 |
300 |
由表中数据可得 ,故我们由此认为 “新措施对防治非典有效” 的把握为( )
,故我们由此认为 “新措施对防治非典有效” 的把握为( )
A.0 B C.
C.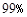 D.
D.
在数列 中,
中, ,当
,当 时,
时,
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设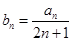 ,求数列
,求数列 的前
的前 项和
项和 .
.
【解析】本试题主要考查了数列的通项公式的求和 综合运用。第一问中 ,利用 ,得到
,得到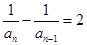 且
且 ,故故
,故故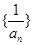 为以1为首项,公差为2的等差数列. 从而
为以1为首项,公差为2的等差数列. 从而

第二问中,


由 及
及 知
知 ,从而可得
,从而可得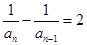 且
且
故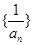 为以1为首项,公差为2的等差数列.
为以1为首项,公差为2的等差数列.
从而
 ……………………6分
……………………6分
(2)
 ……………………9分
……………………9分

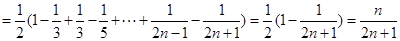
. 在研究某新措施对“非典”的k*s#5^u防治效果问题时,得到如![]() 下列联表:
下列联表:
| 存活数 | 死亡数 | 合计 | |
| 新措施 | 132 | 18 | 150 |
| 对照 | 114 | 36 | 150 |
| 合计 | 246 | 54 | 300 |
由表中数据可得![]() ,故我们由此认为 “新措施对防治非典有效” 的k*s#5^u把握为( )
,故我们由此认为 “新措施对防治非典有效” 的k*s#5^u把握为( )
A.0 ![]() B
B![]() C.
C.![]() D.
D.![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com