27．已知:B.C是线段AD上的两点.且AB＝CD.分别以AB.BC.CD.AD为直径作四个半圆.得到一个如图所示的轴对称图形．此图的对称轴分别交其中两个半圆于M.N.交AD于O．若AD＝16.AB＝——青夏教育精英家教网—

27．已知:B.C是线段AD上的两点.且AB＝CD.分别以AB.BC.CD.AD为直径作四个半圆.得到一个如图所示的轴对称图形．此图的对称轴分别交其中两个半圆于M.N.交AD于O．若AD＝16.AB＝2r.回答下列问题: (1)用含r的代数式表示BC＝ .MN＝ , (2)设以MN为直径的圆的面积为S.阴影部分的面积为S阴影.请通过计算填写下表:rSS阴影r＝1 49πr＝236π r＝3 25π (3)由此猜想S与S阴影的大小关系.并证明你的猜想．【查看更多】

题目列表(包括答案和解析)

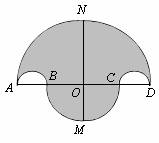
已知：B、C是线段AD上的两点，且AB＝CD，分别以AB、BC、CD、AD为直径作四个半圆，得到一个如图所示的轴对称图形．此图的对称轴分别交其中两个半圆于M、N，交AD于O．若AD＝16，AB＝2r(0＜r＜4），回答下列问题：

（1）用含r的代数式表示BC＝____________，MN＝____________；

（2）设以MN为直径的圆的面积为S，阴影部分的面积为S_阴影，请通过计算填写下表：

r	S	S阴影
r＝1		49π
r＝2	36π
r＝3		25π

（3）由此猜想S与S_阴影的大小关系，并证明你的猜想．

查看答案和解析>>

已知A、D是一段圆弧上的两点，且在直线l的同侧，分别过这两点作l的垂线，垂足为B、C，E是BC上一动点，连结AD、AE、DE，且∠AED＝90°．

(1)如图①，如果AB＝6，BE＝4，CE＝12求CD的长．

(2)如图②，若点E恰为这段圆弧的圆心，则线段AB、BC、CD之间有怎样的等量关系？请写出你的结论并予以证明．再探究：当A、D分别在直线l两侧且AB≠CD，而其余条件不变时，线段AB、BC、CD之间又有怎样的等量关系？请直接写出结论，不必证明．

查看答案和解析>>

已知：B、C是线段AD上的两点，且AB＝CD，分别以AB、BC、CD、AD为直径作四个半圆，得到一个如图所示的轴对称图形．此图的对称轴分别交其中两个半圆于M、N，交AD于O．若AD＝16，AB＝2r(0＜r＜4)，回答下列问题：

(1)用含r的代数式表示BC＝________，MN＝________；

(2)设以MN为直径的圆的面积为S，阴影部分的面积为S_阴影，请通过计算填写下表：

(3)由此猜想S与S_阴影的大小关系，并证明你的猜想．

查看答案和解析>>

阅读与证明：
如图，已知正方形ABCD中，E、F分别是CD、BC上的点，且∠EAF＝45 °，
求证：BF＋DE＝EF。
分析：证明一条线段等于另两条线段的和，常用“截长法”或“补短法”，将线段BF、DE放在同一直线上，构造出一条与BF＋DE相等的线段。如图1延长ED至点F'，使DF'＝BF，连接A F'，易证△ABF≌△ADF'，进一步证明△AEF≌△AEF'，即可得结论。
（1）请你将下面的证明过程补充完整。
证明：延长ED至F'，使DF'＝BF，
∵ 四边形ABCD是正方形
∴ AB＝AD，∠ABF＝∠ADF'＝90°，
∴ △ABF≌△ADF'（SAS）
应用与拓展：如图建立平面直角坐标系，使顶点A与坐标原点O重合，边OB、OD分别在x轴、y轴的正半轴上。
（2）设正方形边长OB为30，当E为CD中点时，试问F为BC的几等分点？并求此时F点的坐标；
（3）设正方形边长OB为30，当EF最短时，直接写出直线EF的解析式：。