
题目列表(包括答案和解析)
电子感应加速器是利用变化磁场产生的电场来加速电子的,如图所示.在圆形磁铁的两极之间有一环形真空室,用交变电流充磁的电磁铁在两极间产生交变磁场,从而在环形室内产生很强的电场,使电子加速被加速的电子同时在洛伦兹力的作用下沿圆形轨道运动,没法把高能电子引入靶室,能使其进一步加速在一个半径为r=0.84m的电子感应加速器中,电子在被加速的![]() 时间内获得的能量为120MeV.这期间电子轨道内的高频交变磁场是线性变化的.磁通量从零增到1.8Wb,求:
时间内获得的能量为120MeV.这期间电子轨道内的高频交变磁场是线性变化的.磁通量从零增到1.8Wb,求:
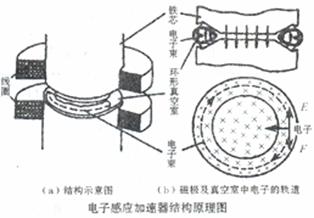
(1) 当交变磁场线性增强时,电子所处的环形真空室内产生的感应电动势大小?
(2) 电子在环形真空室中共绕行了多少周?
(3) 有人说,根据麦克斯韦电磁场理论及法拉第电磁感应定律,电子感应加速器要完成电子的加速过程,电子轨道内的高频交变磁场也可以是线性减弱的,效果将完全一样,你同意吗?请简述理由.

图
A.当ef向右滑动时,左边的面积增大lΔd,右边的面积减少lΔd,电动势应为E=![]()
B.当ef向右滑动时,左边的面积增大lΔd,右边的面积减少lΔd,相互抵消E=0
C.在公式E=![]() 中,切割磁感线的情况下ΔΦ=BΔS,ΔS应为导线切割扫过的面积,故有E=
中,切割磁感线的情况下ΔΦ=BΔS,ΔS应为导线切割扫过的面积,故有E=![]()
D.在切割磁感线的情况下只能用E=Blv来计算,不能用E=![]() 来计算
来计算
如图2所示,两根平行的金属导轨,固定在同一水平面上,磁感应强度B=0.05 T的匀强磁场与导轨所在平面垂直(图中未画出),导轨的电阻很小,可忽略不计.导轨间的距离l=0.20 m.两根质量均为m=0.10 kg的平行金属杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的电阻均为R=0.50 Ω.在t=0时刻,两杆都处于静止状态.现有一与导轨平行、大小为0.20 N的恒力F作用于金属杆甲上,使金属杆在导轨上滑动.经过t=5.0 s,金属杆甲的加速度为a=1.37 m/s2.问此时两金属杆的速度各为多少??
图2
【解析】设t=5.0 s时两金属杆甲、乙之间的距离为x,速度分别为v1和v2,经过很短的时间Δt,杆甲移动距离v1Δt,杆乙移动距离v2Δt,回路面积改变ΔS=[(x-v2Δt)+v1Δt]l-lx=(v1-v2)lΔt.由法拉第电磁感应定律知,回路中的感应电动势回路中的电流
对杆甲由牛顿第二定律有F-BlI=ma
由于作用于杆甲和杆乙的安培力总是大小相等、方向相反,所以t=5.0 s时两杆的动量(t=0时为0)等于外力F的冲量Ft=mv1+mv2
联立以上各式解得
代入数据得v1=8.15 m/s,v2=1.85 m/s.
如图2所示,两根平行的金属导轨,固定在同一水平面上,磁感应强度B=0.05 T的匀强磁场与导轨所在平面垂直(图中未画出),导轨的电阻很小,可忽略不计.导轨间的距离l=0.20 m.两根质量均为m=0.10 kg的平行金属杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的电阻均为R=0.50 Ω.在t=0时刻,两杆都处于静止状态.现有一与导轨平行、大小为0.20 N的恒力F作用于金属杆甲上,使金属杆在导轨上滑动.经过t=5.0 s,金属杆甲的加速度为a=1.37 m/s2.问此时两金属杆的速度各为多少??
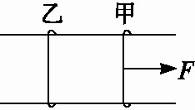
图2
【解析】设t=5.0 s时两金属杆甲、乙之间的距离为x,速度分别为v1和v2,经过很短的时间Δt,杆甲移动距离v1Δt,杆乙移动距离v2Δt,回路面积改变ΔS=[(x-v2Δt)+v1Δt]l-lx=(v1-v2)lΔt.由法拉第电磁感应定律知,回路中的感应电动势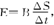 回路中的电流
回路中的电流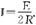
对杆甲由牛顿第二定律有F-BlI=ma
由于作用于杆甲和杆乙的安培力总是大小相等、方向相反,所以t=5.0 s时两杆的动量(t=0时为0)等于外力F的冲量Ft=mv1+mv2
联立以上各式解得
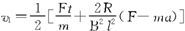

代入数据得v1=8.15 m/s,v2=1.85 m/s.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com