
题目列表(包括答案和解析)
(本小题满分12分)等差数列![]() 中,
中,![]() ,公差
,公差![]() 是自然数,等比数列
是自然数,等比数列![]() 中,
中,![]() (Ⅰ)试找出一个
(Ⅰ)试找出一个![]() 的值,使
的值,使![]() 的所有项都是
的所有项都是![]() 中的项;再找出一个
中的项;再找出一个![]() 的值,使
的值,使![]() 的项不都是
的项不都是![]() 中的项(不必证明);(Ⅱ)判断
中的项(不必证明);(Ⅱ)判断![]() 时,是否
时,是否![]() 所有的项都是
所有的项都是![]() 中的项, 并证明你的结论;(Ⅲ)探索当且仅当
中的项, 并证明你的结论;(Ⅲ)探索当且仅当![]() 取怎样的自然数时,
取怎样的自然数时,![]() 的所有项都是
的所有项都是![]() 中的项,并说明理由.
中的项,并说明理由.
(本小题满分12分)
等差数列 中,前
中,前 项和为
项和为 ,且
,且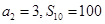 .
.
(Ⅰ)求 通项公式;
通项公式;
(Ⅱ)设 ,求数列
,求数列 前
前 项的和
项的和 .
.
(本小题满分12分)等差数列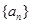 中,
中,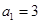 ,前
,前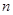 项和为
项和为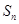 ,等比数列
,等比数列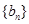 各项均为正数,
各项均为正数, ,且
,且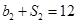 ,
,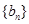 的公比
的公比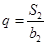
(1)求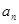 与
与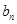 ;
;
(2)求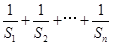
(本小题满分12分)等差数列 中,已知
中,已知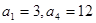 ,
,
(I)求数列 的通项公式;
的通项公式;
(Ⅱ)若 分别为等比数列
分别为等比数列 的第1项和第2项,试求数列
的第1项和第2项,试求数列 的通项公式及前
的通项公式及前
项和 .
.
(本小题满分12分)等差数列 中,
中, ,且
,且 成等比数列,求数列
成等比数列,求数列 前20项的和
前20项的和 .
.
评分说明:
1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要
考查内容比照评分参考制订相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和
难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数.选择题不给中间分.
一、选择题
1.C 2.B 3.D 4.C 5.C 6.D
7.A 8.B 9.A 10.B 11.B 12.C
二、填空题
13.2 14.420 15.2
16.两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.
注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.
1.若且是,则是( )
A.第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
【答案】C
【解析】,在三、四象限;,在一、三象限,∴选C
2.设集合,( )
A. B. C. D.
【答案】B
【解析】,,∴
【高考考点】集合的运算,整数集的符号识别
3.原点到直线的距离为( )
A.1 B. C.2 D.
【答案】D
【解析】
【高考考点】点到直线的距离公式
4.函数的图像关于( )
A.轴对称 B. 直线对称
C. 坐标原点对称 D. 直线对称
【答案】C
【解析】是奇函数,所以图象关于原点对称
【高考考点】函数奇偶性的性质
5.若,则( )
A.<< B. << C. << D. <<
【答案】C
【解析】由,令且取知<<
6.设变量满足约束条件:,则的最小值为( )
A. B. C. D.
【答案】D
于是
7.设曲线在点(1,)处的切线与直线平行,则( )
A.1 B. C. D.
【答案】A
【解析】,于是切线的斜率,∴有
8.正四棱锥的侧棱长为,侧棱与底面所成的角为,则该棱锥的体积为( )
A.3 B.6 C.9 D.18
【答案】B
【解析】高,又因底面正方形的对角线等于,∴底面积为
,∴体积
【备考提示】在底面积的计算时,要注意多思则少算
9.的展开式中的系数是( )
A. B. C.3 D.4
【答案】A
【解析】
【易错提醒】容易漏掉项或该项的负号
10.函数的最大值为( )
A.1 B. C. D.2
【答案】B
【解析】,所以最大值是
【高考考点】三角函数中化为一个角的三角函数问题
【备考提示】三角函数中化为一个角的三角函数问题是三角函数在高考中的热点问题
11.设是等腰三角形,,则以为焦点且过点的双曲线的离心率为( )
A. B. C. D.
【答案】B
【解析】由题意,所以,由双曲线的定义,有
,∴
【高考考点】双曲线的有关性质,双曲线第一定义的应用
12.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )
A.1 B. C. D.2
【答案】C
【解析】设两圆的圆心分别为、,球心为,公共弦为AB,其中点为E,则为矩形,于是对角线,而,∴
【高考考点】球的有关概念,两平面垂直的性质
13.设向量,若向量与向量共线,则 .
【答案】 2
【解析】=则向量与向量共线
14.从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答)
【答案】 420
【解析】
15.已知是抛物线的焦点,是上的两个点,线段AB的中点为,则的面积等于 .
【答案】 2
【解析】设过M的直线方程为,由
∴,,由题意,于是直线方程为
,,∴,焦点F(1,0)到直线的距离
∴的面积是2
16.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:
充要条件① ;
充要条件② .
(写出你认为正确的两个充要条件)
【答案】两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.
注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.
三、解答题
17.解:
(Ⅰ)由,得,
由,得.??????????????????????????????????????????????????????????????????????????????????????? 2分
所以.??????????????????????????????????????????? 5分
(Ⅱ)由正弦定理得.?????????????????????????????????????????????????? 8分
所以的面积.????????????????????????? 10分
18.解:
设数列的公差为,则
,
,
.????????????????????????????????????????????????????????????????????????????????????????????? 3分
由成等比数列得,
即,
整理得,
解得或.???????????????????????????????????????????????????????????????????????????????????????????????????? 7分
当时,.????????????????????????????????????????????????????????????????????????????????? 9分
当时,,
于是.????????????????????????????????????????????????????? 12分
19.解:
记分别表示甲击中9环,10环,
分别表示乙击中8环,9环,
表示在一轮比赛中甲击中的环数多于乙击中的环数,
表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数,
分别表示三轮中恰有两轮,三轮甲击中环数多于乙击中的环数.
(Ⅰ),????????????????????????????????????????????????????????????????????????????? 2分
.??????????????????????????????????????????????????????????????????????? 6分
(Ⅱ),???????????????????????????????????????????????????????????????????????????????????????????????????? 8分
,
,
.????????????????????????????????? 12分
20.解法一:
依题设,,.
(Ⅰ)连结交于点,则.
由三垂线定理知,.???????????????????????????????????????????????????????????????????????????????????? 3分
由于,
故,,
与互余.
于是.
与平面内两条相交直线都垂直,
所以平面.??????????????????????????????????????????????????????????????????????????????????????????????? 6分
(Ⅱ)作,垂足为,连结.由三垂线定理知,
故是二面角的平面角.????????????????????????????????????????????????????????????????? 8分
,
,.
,.
又,.
.
解法二:
以为坐标原点,射线为轴的正半轴,
建立如图所示直角坐标系.
依题设,.
,.?????????????????????????????????? 3分
(Ⅰ)因为,,
故,.
又,
所以平面.??????????????????????????????????????????????????????????????????????????????????????????????? 6分
(Ⅱ)设向量是平面的法向量,则
,.
故,.
令,则,,.?????????????????????????????????????????????????????????????? 9分
等于二面角的平面角,
.
所以二面角的大小为.????????????????????????????????????????????????????????? 12分
21.解:
(Ⅰ).
因为是函数的极值点,所以,即,因此.
经验证,当时,是函数的极值点.??????????????????????????????????????????????? 4分
(Ⅱ)由题设,.
当在区间上的最大值为时,
,
即.
故得.??????????????????????????????????????????????????????????????????????????????????????????????????????????????? 9分
反之,当时,对任意,
,
而,故在区间上的最大值为.
综上,的取值范围为.??????????????????????????????????????????????????????????????????????????????? 12分
22.(Ⅰ)解:依题设得椭圆的方程为,
直线的方程分别为,.???????????????????????????????????????????? 2分
如图,设,其中,
故.①
由知,得;
由在上知,得.
所以,
化简得,
解得或.??????????????????????????????????????????????????????????????????????????????????????????????????? 6分
(Ⅱ)解法一:根据点到直线的距离公式和①式知,点到的距离分别为,
.???????????????????????????????????????????????????????????????? 9分
又,所以四边形的面积为
,
当,即当时,上式取等号.所以的最大值为.????????????????????????????? 12分
解法二:由题设,,.
设,,由①得,,
故四边形的面积为
???????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 9分
,
当时,上式取等号.所以的最大值为.?????????????????????????????????????????????? 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com