
题目列表(包括答案和解析)
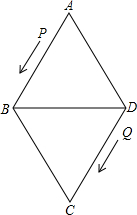 点D同时出发沿线路DC→CB→BA作匀速运动.
点D同时出发沿线路DC→CB→BA作匀速运动.

现将连续自然数1至2009按图中的方式排列成一个长方形队列,再用正方形任意框出16个数。
| | | | |
| | | | |
| | | | |
| | | | |
|
 ,请用
,请用 的代数式表示该框中的16个数,然后填入右表中相应的空格处,并求出这16个数中的最小数和最大数,然后填入右表中相应的空格处,并求出这16个数的和。(用
的代数式表示该框中的16个数,然后填入右表中相应的空格处,并求出这16个数中的最小数和最大数,然后填入右表中相应的空格处,并求出这16个数的和。(用 的代数式表示)
的代数式表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com