
题目列表(包括答案和解析)
如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为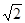 ,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n
,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n

(1)请在图1中找出两对相似而不全等的三角形,并选取其中一对证明它们相似;
(2)根据图1,求m与n的函数关系式,直接写出自变量n的取值范围;
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2). 旋转∆AFG,使得BD=CE,求出D点的坐标,并通过计算验证 ;
;
(4)在旋转过程中,(3)中的等量关系 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.
如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD![]() +CE
+CE![]() =DE
=DE![]() .
.
(4)在旋转过程中,(3)中的等量关系BD![]() +CE
+CE![]() =DE
=DE![]() 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.


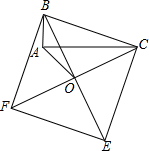 如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6| 2 |
 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=2
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=2| 2 |
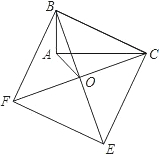 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6| 2 |
| A、12 | ||
| B、16 | ||
C、4
| ||
D、8
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com