
题目列表(包括答案和解析)
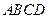 中,
中, ,
,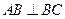 ,以
,以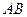 为直径的
为直径的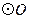 与
与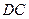 相切于
相切于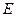 .已知
.已知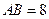 ,边
,边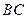 比
比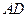 大6.
大6.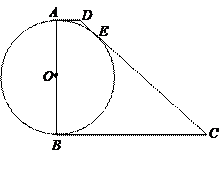
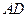 、
、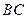 的长.
的长.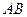 上是否存在一动点
上是否存在一动点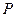 ,使以
,使以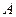 、
、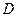 、
、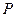 为顶点的三角形与
为顶点的三角形与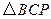 相似?若存在,求出
相似?若存在,求出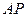 的长;若不存在,请说明理由.
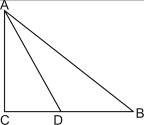
的长;若不存在,请说明理由.(本小题满分6分)已知:如图,在![]() 中,
中,![]() D是BC上的点,
D是BC上的点,![]() .求AC(
.求AC(![]() ,结果保留整数).
,结果保留整数).
(本小题满分8分)
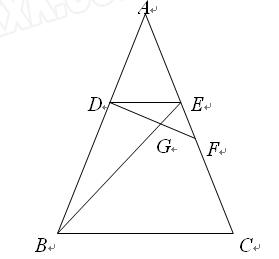
已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交 于点G,且∠EDF=∠ABE.
于点G,且∠EDF=∠ABE.
求证:(1)△DEF∽△BDE;
(2) .
.
.(本小题满分12分)
如图,已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连结AF交CE于H,连结AC、CF、BF。
1.(1)请你找出图中的相似三角形,并对其中的一对相似三角形进行证明;
2.(2)若AE:BE=1:4,求CD长。
3.(3)在(2)的条件下,求![]() 的值。
的值。
(本小题满分12分)
如图(1)在Rt△ACB中,∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1 cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ。若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题:
(1)当t为何值时,以A、P、Q为顶点的三角形与△ABC相似?
(2)设四边形PQCB的面积为y(![]() ),直接写出y与t之间的函数关系式;
),直接写出y与t之间的函数关系式;
(3)在点P、点Q的移动过程中,如果将△APQ沿其一边所在直线翻折,翻折后的三角形与△APQ组成一个四边形,那么是否存在某一时刻t,使组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.
图(1) 备用图 备用图
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com