
题目列表(包括答案和解析)
已知数列![]() 中,
中,![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() .令
.令![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求证:
,求证:![]() (
(![]() ).
).
 中,
中, ,
, ,其前
,其前 项和
项和 满足
满足 .令
.令 .
. 的通项公式;
的通项公式; ,求证:
,求证: (
( ).
).
已知数列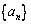 中,
中,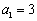 ,
,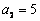 ,其前
,其前 项和
项和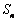 满足
满足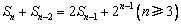 .令
.令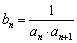 .
.
(Ⅰ)求数列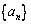 的通项公式;
的通项公式;
(Ⅱ)若 ,求证:
,求证: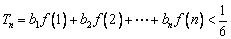 (
(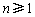 );
);
(Ⅲ)令 (
(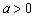 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有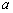 的值:①对于任意正整数
的值:①对于任意正整数 ,都有
,都有 ;②对于任意的
;②对于任意的 ,均存在
,均存在 ,使得
,使得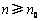 时,
时,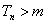 .
.
已知数列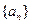 中,
中,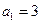 ,
, ,其前
,其前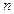 项和
项和 满足
满足
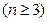 ,令
,令 .
.
(Ⅰ)求数列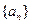 的通项公式;
的通项公式;
(Ⅱ)令 ,求证:
,求证:
① 对于任意正整数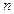 ,都有
,都有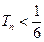 ;
;
② 对于任意的 ,均存在
,均存在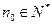 ,使得
,使得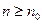 时,
时,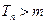 .
.
已知数列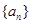 中,
中, ,
,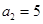 ,其前
,其前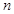 项和
项和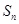 满足
满足
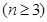 ,令
,令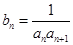 .
.
(Ⅰ)求数列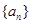 的通项公式;
的通项公式;
(Ⅱ)令 ,求证:
,求证:
① 对于任意正整数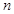 ,都有
,都有 ;
;
② 对于任意的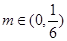 ,均存在
,均存在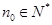 ,使得
,使得 时,
时, .
.
一、选择题: C C D B D A A C B B A D

(2)由(Ⅰ) ,
, .
.
 的可能取值为:
的可能取值为: 、
、 、
、 、
、 .
.
则 ;
;
 ;
;
 ;
;
 .…………9分
.…………9分
∴ 的分布列为
的分布列为










 的数学期望
的数学期望 .…………12分
.…………12分
 故二面角
故二面角 的大小为
的大小为 …………………………12分
…………………………12分

解法二:如图,以 为原点,建立空间直角坐标系,使
为原点,建立空间直角坐标系,使 轴,
轴, 、
、 分别在
分别在 轴、
轴、 轴上。
轴上。

20.解:(1)由题意知 即
即 ……2分
……2分
∴
 ……5分
……5分
检验知 、
、 时,结论也成立,故
时,结论也成立,故 .…………6分
.…………6分
(2)由于 ,故
,故

 .…………12分
.…………12分
21.解:(1)设 ,由
,由 知:R是TN的中点,…………………1分
知:R是TN的中点,…………………1分
则T(-x,0),R(0,
 ),
), =O 则(-x,-
=O 则(-x,-  )?(1,-
)?(1,-  )=0………………3分
)=0………………3分
∴ 点N的轨迹曲线C的方程为: ……………5分
……………5分
(2)设直线 的方程为
的方程为 ,代入曲线C的方程
,代入曲线C的方程 得:
得:  此方程有两个不等实根,
此方程有两个不等实根,
 ……………6分
……………6分
M在曲线C上,P、Q是直线 与曲线C的交点,
与曲线C的交点,
设 则
则 ,
,
 是以PQ为斜边的直角三角形
是以PQ为斜边的直角三角形 ……8分
……8分
 ,
, ,有
,有
由于 ,
,
∴ ∴
∴ …………10分
…………10分
t为点M的纵坐标, 关于
关于 的方程
的方程 有实根,
有实根,

 ,
,
直线 的斜率
的斜率 且
且 ,
, 或
或 …12分
…12分
22.解(1)
∴ 的增区间为
的增区间为 ,
, 减区间为
减区间为 和
和 .…………3分
.…………3分
极大值为 ,极小值为
,极小值为 .…………5分
.…………5分
(2)原不等式可化为 由(1)知,
由(1)知, 时,
时, 的最大值为
的最大值为 .
.
∴ 的最大值为
的最大值为 ,由恒成立的意义知道
,由恒成立的意义知道 ,从而
,从而 …8分
…8分
(3)设
则 .
.
∴当 时,
时, ,故
,故 在
在 上是减函数,
上是减函数,
又当 、
、 、
、 、
、 是正实数时,
是正实数时,
∴ .
.
由 的单调性有:
的单调性有: ,
,
即 .…………12′
.…………12′
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com