
题目列表(包括答案和解析)
| 3 |
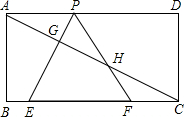 三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.已知如图所示,点(1,3)在函数![]() 的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数
的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数![]() 的图象又经过A、E两点,点E的横坐标为m,解答下列各题:
的图象又经过A、E两点,点E的横坐标为m,解答下列各题:

(1)求k的值;
(2)求点C的横坐标(用m表示);
(3)当∠ABD=45°时,求m的值.
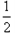 x与直线l2:y= -x+6相交于点M,直线l2与x轴相交于点N.
x与直线l2:y= -x+6相交于点M,直线l2与x轴相交于点N. C=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动,设矩形ABCD与△OMN的重叠部分的面积为S,移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时开始结束).直接写出S与自变量t之间的函数关系式(不需要给出解答过程).
C=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动,设矩形ABCD与△OMN的重叠部分的面积为S,移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时开始结束).直接写出S与自变量t之间的函数关系式(不需要给出解答过程).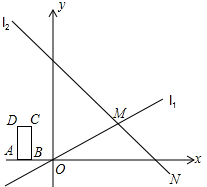
如图,在平面直角坐标系xOy中,已知直线l1:y=![]() x与直线l2:y= -x+6相交于点M,直线l2与x轴相交于点N.
x与直线l2:y= -x+6相交于点M,直线l2与x轴相交于点N.
(1)求M,N的坐标.
(2)矩形ABCD中,已知AB=1,B![]() C=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动,设矩形ABCD与△OMN的重叠部分的面积为S,移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时开始结束).直接写出S与自变量t之间的函数关系式(不需要给出解答过程).
C=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动,设矩形ABCD与△OMN的重叠部分的面积为S,移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时开始结束).直接写出S与自变量t之间的函数关系式(不需要给出解答过程).
(3)在(2)的条件下,当t为何值时,S的值最大?并求出最大值.

 x与直线l2:y=-x+6相交于点M,直线l2与x轴相交于点N.
x与直线l2:y=-x+6相交于点M,直线l2与x轴相交于点N.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com