2．描点:以表中各对对应值为坐标.在坐标系中画出各点．——青夏教育精英家教网—

2．描点:以表中各对对应值为坐标.在坐标系中画出各点．【查看更多】

(1)根据y＝2x(x≥0)填写下表：

(2)分别以每个x的值为横坐标，以对应的y值为纵坐标，在直角坐标系中描出各点；

(3)按照横坐标由小到大的顺序，把所描出的各点用平滑的曲线依次连接起来．

我市某工艺厂为配合奥运会，设计了一款成本为20元∕件的工艺品投放市场进行试销．经过调查，得到如下数据：

销售单价x(元/件)	……	30	40	50	60	……
每天销售量y(件)	……	500	400	300	200	……

(1)把上表中x、y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式；

(2)当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？(利润＝销售总价－成本总价)

(3)当地物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？

分析　(1)从表格中的数据我们可以看出当x增加10时，对应y的值减小100，所以y与x之间可能是一次函数的关系，我们可以根据图象发现这些点在一条直线上，所以y与x之间是一次函数的关系，然后设出一次函数关系式，求出其关系式．

(2)利用二次函数的知识求最大值．

查看答案和解析>>

水产公司有一种海产品共2104千克，为寻求合适的销售价格，进行了8天试销，试销情况如下：

	第1天	第2天	第3天	第4天	第5天	第6天	第7天	第8天
售价x（元/千克）	400	300	250	240	______	150	125	120
销售量y（千克）	30	40	48	50	60	______	96	100

（1）以上表中的x、y分别为横坐标、纵坐标建立直角坐标系（在草稿纸上画草图即可），在坐标系内描出x、y各组对应值作为点的坐标，用光滑曲线连接起来，观察所得到的图象，猜测这种海产品的每天销售量y（千克）与销售价格x（元/千克）之间的函数关系式，并求出这个函数关系式．[注：现设定在这批海产品的销售中，每天的销售量y（千克）与销售价格x（元/千克）之间都满足这一关系．]
（2）在试销8天后，水产公司决定在20天内每天按同一售价把这批海产品全部售出．请你帮助公司核定这20天内每天的售价是多少？
（3）在按（2）中定价继续销售15天后，公司发现剩余的这些海产品必须在不超过2天内全部售出，此时需要重新确定一个销售价格，使后面两天都按新的价格销售，那么新确定的价格最高不超过每千克多少元才能完成销售任务？

查看答案和解析>>

（2010•石家庄模拟）水产公司有一种海产品共2104千克，为寻求合适的销售价格，进行了8天试销，试销情况如下：

	第1天	第2天	第3天	第4天	第5天	第6天	第7天	第8天
售价x（元/千克）	400	300	250	240	200 200	150	125	120
销售量y（千克）	30	40	48	50	60	80 80	96	100

（1）以上表中的x、y分别为横坐标、纵坐标建立直角坐标系（在草稿纸上画草图即可），在坐标系内描出x、y各组对应值作为点的坐标，用光滑曲线连接起来，观察所得到的图象，猜测这种海产品的每天销售量y（千克）与销售价格x（元/千克）之间的函数关系式，并求出这个函数关系式．[注：现设定在这批海产品的销售中，每天的销售量y（千克）与销售价格x（元/千克）之间都满足这一关系．]
（2）在试销8天后，水产公司决定在20天内每天按同一售价把这批海产品全部售出．请你帮助公司核定这20天内每天的售价是多少？
（3）在按（2）中定价继续销售15天后，公司发现剩余的这些海产品必须在不超过2天内全部售出，此时需要重新确定一个销售价格，使后面两天都按新的价格销售，那么新确定的价格最高不超过每千克多少元才能完成销售任务？

查看答案和解析>>

如图，李老师设计了一个探究杠杆平衡条件的实验：在一个自制类似天平的仪器的左边固定托盘A中放置一个重物，在右边的活动托盘B(可左右移动)中放置一定质量的砝码，使得仪器左右平衡，改变活动托盘B与点O的距离x(cm)，观察活动托盘B中砝码的质量y(g)的变化情况．实验数据记录如下表：

(1)把上表中(x，y)的各组对应值作为点的坐标，在坐标系中描出相应的点，用平滑曲线连接这些点；

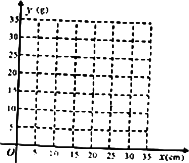
(2)观察所画的图象，猜测y与x之间的函数关系，求出函数关系式并加以验证；

(3)当砝码的质量为24 g时，活动托盘B与点O的距离是多少cm？

(4)当活动托盘B往左移动时，应往活动托盘B中添加还是减少砝码？

查看答案和解析>>

练习册

高中

初中

小学