.(本题12分)

已知抛物线y=ax2+bx+c经过P（，3），E（，0）及原点O（0，0）

（1）求抛物线的解析式；

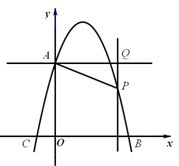
（2）过P点作平行于x轴的直线PC交y轴于C点，在抛物线对称轴右侧

且位于直线PC下方的抛物线上，任取一点Q，过点Q作直线QA平行于y

轴交x轴于A点，交直线PC于B点，直线QA与直线PC及两坐标轴围成矩形OABC（如图）．是否存在点Q，使得△OPC与△PQB相似？若存在，求出Q点的坐标；若不存在，请说明理由；

（3）如果符合（2）中的Q点在x轴的上方，连接OQ，矩形OABC内的四个三角形△OPC，△PQB，△OQP，△OQA之间存在怎样的关系，为什么？

(本题12分) 某商品每件买入价为30元，销售价的25%用于纳税等其他费用，每日销售量P件与销售价x元之间满足关系式：P=-x+100(40＜x＜100).

1.（1）当销售价为60元时，每件商品的纯利润为      元，此时每日销售量为       件.

2.（2）若要使每件商品的纯利润y元保持在买入价的20%--70%（包括20%和70%），问该如何确定销售价？，并求出最大利润. [总利润=每件纯利润×销售量]

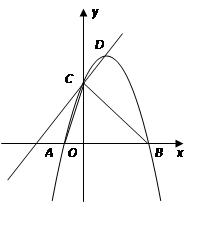
(本题12分) 如图，已知二次函数的图象与轴交于点、，与轴交于点，其顶点为，且直线的解析式为．

1.(1) 求二次函数的解析式．

2.(2) 求△ABC外接圆的半径及外心的坐标；

3.(3) 若点P是第一象限内抛物线上一动点，求四边形ACPB的面积最大值．

(本题12分) 在正方形网格中，A、B为格点，以点为圆心，为半径作圆交网格线于点(如图(1))，过点作圆的切线交网格线于点，以点为圆心，为半径作圆交网格线于点(如图(2))．

问题：

1.(1) 求的度数；

2.(2) 求证：；

3.(3) 可以看作是由经过怎样的变换得到的？并判断的形状(不用说明理由)．

4.(4) 如图(3)，已知直线，且a∥b，b∥c，在图中用直尺、三角板、圆规画等边三角形，使三个顶点，分别在直线上．要求写出简要的画图过程，不需要说明理由．

( 本题12分) 已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E。

求证：1.（1）△BFC≌△DFC；

2.（2）AD=DE