
题目列表(包括答案和解析)
| 1 | 3 |
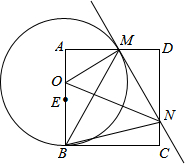 如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是( )
如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是( )| A、S1>S2+S3 | B、△AOM∽△DMN | C、∠MBN=45° | D、MN=AM+CN |
 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N. 时,求
时,求 的值;
的值; 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;
如图,扇形OAB的半径为4,圆心角∠AOB=90°,点C是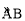 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
(1)当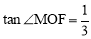 时,求
时,求 的值;
的值;
(2)设OM=x,ON=y,当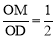 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;
(3)在(2)的条件下,联结CF,当△ECF与△OFN相似时,求OD的长.
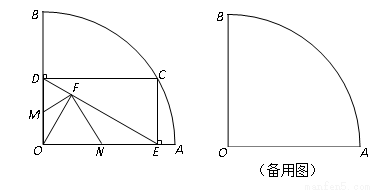
 上,AB边在直线
上,AB边在直线 上.
上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com