
题目列表(包括答案和解析)
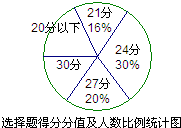 19、在本学期第九周进行的白云区08年初三毕业班中考第一次模拟考试(简称初三“一模”)中,九年级某班50名同学选择题(共10小题,每小题3分,满分30分)的得分情况如下表:
19、在本学期第九周进行的白云区08年初三毕业班中考第一次模拟考试(简称初三“一模”)中,九年级某班50名同学选择题(共10小题,每小题3分,满分30分)的得分情况如下表:| 分 值 | 6 | 12 | 18 | 21 | 24 | 27 | 30 |
| 人 数 | 1 | 2 | 6 | 8 | 15 | 10 | 8 |
| 8 | 5 |
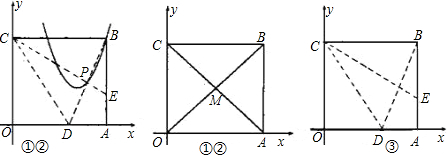

(本小题满分14分)
如图①,已知四边形ABCD是正方形,点E是AB的中点,点F在边CB的延长线上,且BE=BF,连接EF.

1.(1)若取AE的中点P,求证:BP= CF;
CF;
2.(2)在图①中,若将 绕点B顺时针方向旋转
绕点B顺时针方向旋转 (00<
(00< <3600),如图②,是否存在某位置,使得
<3600),如图②,是否存在某位置,使得 ?,若存在,求出所有可能的旋转角
?,若存在,求出所有可能的旋转角 的大小;若不存在,请说明理由;
的大小;若不存在,请说明理由;
3.(3)在图①中,若将△BEF绕点B顺时针旋转 (00<
(00< <900),如图③,取AE的中点P,连接BP、CF,求证:BP=
<900),如图③,取AE的中点P,连接BP、CF,求证:BP= CF且BP⊥CF.
CF且BP⊥CF.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com