
题目列表(包括答案和解析)
观察可得最简公分母是(x+1)(x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【解答】
(2)方程的两边同乘(x+1)(x-1),得
2(x-1)+4=x2-1,
即x2-2x-3=0,
(x-3)(x+1)=0,
解得x1=3,x2=-1,
检验:把x=3代入(x+1)(x-1)=8≠0,即x=3是原分式方程的解,
把x=-1代入(x+1)(x-1)=0,即x=-1不是原分式方程的解,
则原方程的解为:x=3.
【点评】此题考查了![]() 实数的混合运算与分式方程的解法.此题难度不大,但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,注意解分式方程一定要验根.
实数的混合运算与分式方程的解法.此题难度不大,但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,注意解分式方程一定要验根.
20.(本题满分5分)如图,已知△ABC,且∠ACB=90°。
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明);
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系(不必证明).
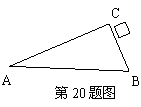 |
(本题满分10分)如图,已知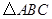 ,以
,以 为直径,
为直径,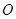 为圆心的半圆交
为圆心的半圆交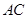 于点
于点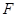 ,点
,点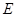 为弧CF的中点,连接
为弧CF的中点,连接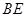 交
交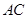 于点
于点 ,
, 为△ABC的角平分线,且
为△ABC的角平分线,且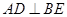 ,垂足为点
,垂足为点 . [来源:]
. [来源:]
(1)求证: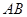 是半圆
是半圆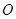 的切线;
的切线;
(2)若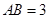 ,
,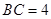 ,求
,求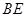 的长.
的长.
(本题满分8分)
如图,已知一次函数与反比例函数的图象交于点P(-2,-1)和点Q(1,m)
(1)求这两个函数的关系式;
(2)根据图象,直接写出当一次函数的值大于反比例函数的值时自变量x的取值范围.

(本题满分12分)如图,已知直线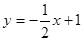 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
【小题1】(1)填空:点A的坐标为 ,点B的坐标为 ,AB的长为 .
【小题2】(2)求点C、D的坐标
【小题3】(3)求抛物线的解析式
【小题4】(4)若抛物线与正方形沿射线AB下滑,直至点C落在 轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为 .
轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为 .
(本题满分12分)如图,已知直线 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
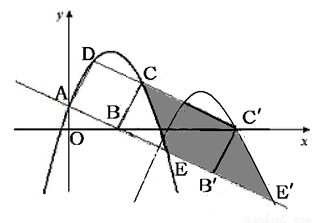
1.(1)填空:点A的坐标为 ,点B的坐标为 ,AB的长为 .
2.(2)求点C、D的坐标
3.(3)求抛物线的解析式
4.(4)若抛物线与正方形沿射线AB下滑,直至点C落在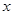 轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为
.
轴上时停止,则抛物线上C、E两点间的抛物线所扫过的面积为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com