
题目列表(包括答案和解析)
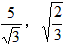 ,
,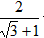 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: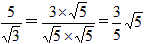 ;(一)
;(一)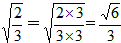 (二)
(二)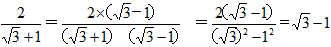 (三)
(三)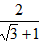 还可以用以下方法化简:
还可以用以下方法化简: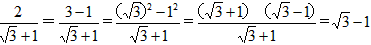 (四)
(四)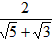 ;
;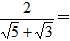 ____;
____;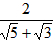 =____;
=____;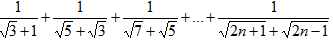 。
。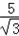 ,
, ,
,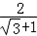 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: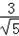 =
= =
= ;
; =
=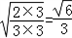
 =
= =
=
 还可以用以下方法化简:
还可以用以下方法化简: =
=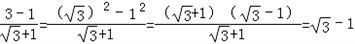
 。
。 =( );
=( ); =( )。
=( )。 。
。阅读下列材料,然后回答问题。
在进行二次根式去处时,我们有时会碰上如![]() ,
,![]() ,
,![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简:
![]() =
=![]() ;(一)
;(一)
![]() =
=![]() (二)
(二)
![]() =
=![]()
![]() =
=![]() (三)
(三)
以上这种化简的步骤叫做分母有理化。
![]() 还可以用以下方法化简:
还可以用以下方法化简:
![]() =
=![]() (四)
(四)
请用不同的方法化简![]() 。
。
参照(三)式得![]() =_____________________________________________;
=_____________________________________________;
‚参照(四)式得![]() =_________________________________________。
=_________________________________________。
(2)化简:![]() 。
。
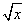 的有理化因式是
的有理化因式是 ,
,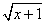 的有理化因式是
的有理化因式是 ,x
,x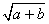 的有理化因式是
的有理化因式是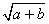 。
。 =12-2=10;
=12-2=10;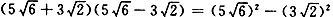 =150-18=132;
=150-18=132;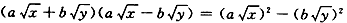 =a2x-b2y。
=a2x-b2y。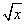 +b
+b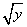 乘a
乘a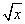 -b
-b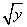 ,其积是有理数,由此我们可以得出:
,其积是有理数,由此我们可以得出: -3
-3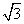 的有理化因式是_______;
的有理化因式是_______;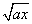 +4
+4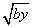 的有理化因式是_______;
的有理化因式是_______;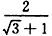 ;
; 。
。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com