
题目列表(包括答案和解析)
 |+(
|+( -tan β)2=0,则此三角形的形状是
-tan β)2=0,则此三角形的形状是
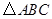 中,点
中,点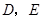 分别在
分别在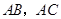 上,设
上,设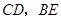 相交于点
相交于点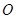 ,若
,若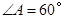 ,
,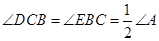 .请你写出图中一个与
.请你写出图中一个与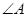 相等的角,并猜想图中哪个四边形是等对边四边形;
相等的角,并猜想图中哪个四边形是等对边四边形;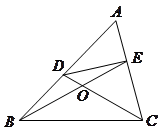
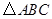 中,如果
中,如果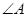 是不等于
是不等于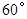 的锐角,点
的锐角,点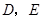 分别在
分别在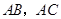 上,且
上,且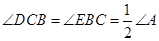 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
【小题1】请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
【小题2】如图,在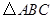 中,点
中,点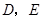 分别在
分别在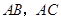 上,设
上,设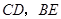 相交于点
相交于点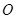 ,若
,若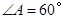 ,
,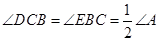 .请你写出图中一个与
.请你写出图中一个与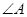 相等的角,并猜想图中哪个四边形是等对边四边形;
相等的角,并猜想图中哪个四边形是等对边四边形;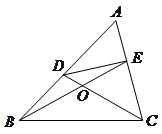
【小题3】在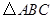 中,如果
中,如果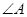 是不等于
是不等于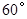 的锐角,点
的锐角,点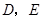 分别在
分别在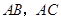 上,且
上,且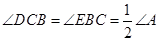 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
我们知道:有两条边相等的三角形叫做等腰三角形。类似地,我们定义:至少有一级对边相等的四边形叫做等对边四边形。
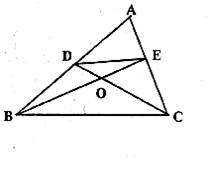
(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
(2)如图,在A ABC中,点D、E分别在AB、AC上,设CD、BE相交于点O,若∠A=60°,∠DCB=∠EBC=![]() ∠A,请写出图中一个与∠A相等的角.并猜想图中哪个四边形是等对边四形;
∠A,请写出图中一个与∠A相等的角.并猜想图中哪个四边形是等对边四形;
(3)在△ABC中,如果∠A是不等于60°的锐角,占D、E分别在AB、AC上,且∠DCB=∠EBC=![]() ∠A,探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论。
∠A,探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com