（本小题满分10分）

    学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.

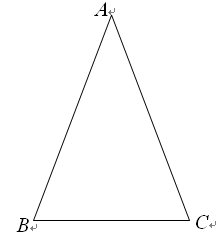
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.

根据上述对角的正对定义，解下列问题：

（1）sad 的值为（   ）A.       B.1  C.      D.2

（2）对于，∠A的正对值sad A的取值范围是        .

（3）已知，其中为锐角，试求sad的值.

（本小题满分5分）

小明想把一个三角形拼接成面积与它相等的矩形．他先进行了如下部分操作，如图1所示：

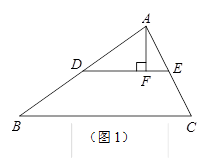
①取△ABC的边AB、AC的中点D、E，联结DE；

   ②过点A作AF⊥DE于点F；

（1）请你帮小明完成图1的操作，把△ABC拼接成面积与它相等的矩形．

（2）若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形，那么原三角形的一边与这边上的高之间的数量关系是________________．

（3）在下面所给的网格中画出符合（2）中条件的三角形，并将其拼接成面积与它相等的正方形．

（本小题满分5分）

小明想把一个三角形拼接成面积与它相等的矩形．他先进行了如下部分操作，如图1所示：

①取△ABC的边AB、AC的中点D、E，联结DE；

②过点A作AF⊥DE于点F；

（1）请你帮小明完成图1的操作，把△ABC拼接成面积与它相等的矩形．

（2）若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形，那么原三角形的一边与这边上的高之间的数量关系是________________．

（3）在下面所给的网格中画出符合（2）中条件的三角形，并将其拼接成面积与它相等的正方形．