
题目列表(包括答案和解析)
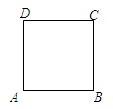 20、如图,有一个边长为5的正方形纸片ABCD,要将其剪拼成边长分别为a,b的两个小正方形,使得a2+b2=52.
20、如图,有一个边长为5的正方形纸片ABCD,要将其剪拼成边长分别为a,b的两个小正方形,使得a2+b2=52.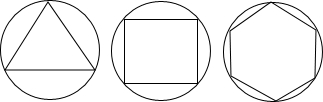 法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.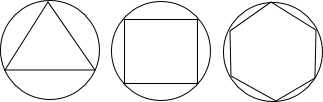 法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.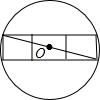 要将三个边长为1的正方形放在一个圆碟内,要求这三个正方形不能有某部分在碟边以外,且不能重叠,问圆碟的半径至少是多少?(如图就是一种放法,此时圆碟的直径至少是长方形对角线,即
要将三个边长为1的正方形放在一个圆碟内,要求这三个正方形不能有某部分在碟边以外,且不能重叠,问圆碟的半径至少是多少?(如图就是一种放法,此时圆碟的直径至少是长方形对角线,即| 10 |
| ||
| 2 |
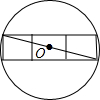 要将三个边长为1的正方形放在一个圆碟内,要求这三个正方形不能有某部分在碟边以外,且不能重叠,问圆碟的半径至少是多少?(如图就是一种放法,此时圆碟的直径至少是长方形对角线,即
要将三个边长为1的正方形放在一个圆碟内,要求这三个正方形不能有某部分在碟边以外,且不能重叠,问圆碟的半径至少是多少?(如图就是一种放法,此时圆碟的直径至少是长方形对角线,即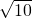 ,故半径至少是
,故半径至少是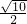 ),请你设计一种,并通过计算指出你认为半径最小的设计方案(画出图)
),请你设计一种,并通过计算指出你认为半径最小的设计方案(画出图)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com