
题目列表(包括答案和解析)
已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 是线段
是线段![]() 上的一点,
上的一点,![]() ,且点M在直线
,且点M在直线![]() 上
上
(1)求椭圆的离心率;
(2)若椭圆的焦点关于直线![]() 的对称点在单位圆
的对称点在单位圆![]() 上,求椭圆的方程
上,求椭圆的方程
已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 是线段
是线段![]() 上的一点,
上的一点,![]() ,且点M在直线
,且点M在直线![]() 上,(1)求椭圆的离心率;(2)若椭圆的焦点关于直线
上,(1)求椭圆的离心率;(2)若椭圆的焦点关于直线![]() 的对称点在单位圆
的对称点在单位圆![]() 上,求椭圆的方程.
上,求椭圆的方程.
已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 是线段
是线段![]() 上的一点,
上的一点,![]() ,且点M在直线
,且点M在直线![]() 上,(1)求椭圆的离心率;(2)若椭圆的焦点关于直线
上,(1)求椭圆的离心率;(2)若椭圆的焦点关于直线![]() 的对称点在单位圆
的对称点在单位圆![]() 上,求椭圆的方程。
上,求椭圆的方程。
已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 是线段
是线段![]() 上的一点,
上的一点,![]() ,且点M在直线
,且点M在直线![]() 上,(1)求椭圆的离心率;(2)若椭圆的焦点关于直线
上,(1)求椭圆的离心率;(2)若椭圆的焦点关于直线![]() 的对称点在单位圆
的对称点在单位圆![]() 上,求椭圆的方程。
上,求椭圆的方程。
已知直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,若椭圆的离心率为
两点,若椭圆的离心率为 ,焦距为2,则线段
,焦距为2,则线段 的长是( )
的长是( )
A. | B.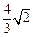 | C. | D. |
一、选择题(本大题共12小题,每小题5分,共60分)
ACBAC ACDAD BC
二、填空题(本大题共4小题,每小题4分,共16分)
13.-----文科数学.files/image248.gif) 14.0 15.300 16.4
14.0 15.300 16.4
三、解答题(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤)
17.解:(1)-----文科数学.files/image250.gif)
-----文科数学.files/image252.gif)
周期-----文科数学.files/image254.gif) ;
;
-----文科数学.files/image256.gif) ,
,
解得单调递增区间为-----文科数学.files/image258.gif)
(2)-----文科数学.files/image174.gif) ,所以
,所以-----文科数学.files/image261.gif) ,
,
-----文科数学.files/image263.gif)
所以-----文科数学.files/image169.gif) 的值域为[2,3]
的值域为[2,3]
而-----文科数学.files/image266.gif) ,所以
,所以-----文科数学.files/image268.gif) ,即
,即-----文科数学.files/image270.gif)
18.解:(1)-----文科数学.files/image272.gif)
-----文科数学.files/image274.gif) 当
当-----文科数学.files/image276.gif) 时,
时,-----文科数学.files/image278.gif)
两式相减得-----文科数学.files/image280.gif)
即-----文科数学.files/image282.gif)
-----文科数学.files/image274.gif) 当
当-----文科数学.files/image276.gif) 时,数列
时,数列-----文科数学.files/image032.gif) 是等比数列
是等比数列
要使数列-----文科数学.files/image032.gif) 是等比数列,
是等比数列,
当且仅当-----文科数学.files/image288.gif) ,即
,即-----文科数学.files/image290.gif)
从而-----文科数学.files/image292.gif)
(2)设数列-----文科数学.files/image185.gif) 的公差为
的公差为-----文科数学.files/image295.gif)
由-----文科数学.files/image190.gif) 得
得-----文科数学.files/image298.gif)
故可设-----文科数学.files/image300.gif)
又-----文科数学.files/image302.gif)
由题意知-----文科数学.files/image304.gif)
解得-----文科数学.files/image306.gif)
又等差数列-----文科数学.files/image185.gif) 的前
的前-----文科数学.files/image160.gif) 项和
项和-----文科数学.files/image188.gif) 有最大值,
有最大值,
-----文科数学.files/image311.gif)
从而-----文科数学.files/image313.gif)
19.解:(1)甲乙二人抽到的牌的所有情况(方片4用
(2,3)、(2,4)、(2,
(4,2)、(4,3)、(4,
共12种不同情况
(没有写全面时:只写出1个不给分,2―4个给1分,5―8个给2分,9―11个给3分)
(2)甲抽到3,乙抽到的牌只能是2,4,
因此乙抽到的牌的数字大于3的概率为-----文科数学.files/image315.gif)
(3)由甲抽到的牌比乙大的有
(3,2)、(4,2)、(4,3)、(
甲胜的概率-----文科数学.files/image317.gif) ,乙获胜的概率为
,乙获胜的概率为-----文科数学.files/image319.gif)
-----文科数学.files/image274.gif) 此游戏不公平。
此游戏不公平。
-----文科数学.files/image322.jpg) 20.证明:由多面体
20.证明:由多面体-----文科数学.files/image199.gif) 的三视图知,四棱锥
的三视图知,四棱锥-----文科数学.files/image199.gif) 的底面
的底面-----文科数学.files/image326.gif) 是长边为2的正方形,侧面
是长边为2的正方形,侧面-----文科数学.files/image213.gif) 是等腰三角形,
是等腰三角形,-----文科数学.files/image329.gif) ,
,
且平面-----文科数学.files/image331.gif) 平面
平面-----文科数学.files/image326.gif)
(1)连结-----文科数学.files/image334.gif) 则
则-----文科数学.files/image203.gif) 是
是-----文科数学.files/image337.gif) 的中点,
的中点,
在-----文科数学.files/image339.gif) 中,
中,-----文科数学.files/image341.gif) ,
,
且-----文科数学.files/image343.gif) 平面
平面-----文科数学.files/image345.gif) 平面
平面-----文科数学.files/image213.gif) ,
,
-----文科数学.files/image348.gif) 平面
平面-----文科数学.files/image213.gif)
(2)因为平面-----文科数学.files/image331.gif) 平面
平面-----文科数学.files/image326.gif) ,
,
平面-----文科数学.files/image353.gif) 平面
平面-----文科数学.files/image355.gif) ,
,
又-----文科数学.files/image357.gif) ,所以,
,所以,-----文科数学.files/image359.gif) 平面
平面-----文科数学.files/image213.gif) ,
,
又-----文科数学.files/image362.gif) 平面
平面-----文科数学.files/image364.gif) ,
,
所以 平面-----文科数学.files/image331.gif) 平面
平面-----文科数学.files/image367.gif)
(3)由三视图知点-----文科数学.files/image043.gif) 到平面
到平面-----文科数学.files/image326.gif) 的距离为1,
的距离为1,
则-----文科数学.files/image371.gif)
21.解:(1)-----文科数学.files/image373.gif) ,即
,即-----文科数学.files/image375.gif) ,
,-----文科数学.files/image377.gif)
-----文科数学.files/image379.gif) 的两根为
的两根为-----文科数学.files/image381.gif)
-----文科数学.files/image383.gif) 有极大值点
有极大值点-----文科数学.files/image385.gif) ,极小值点
,极小值点-----文科数学.files/image222.gif)
此时-----文科数学.files/image169.gif) 在
在-----文科数学.files/image389.gif) 上是减函数,在
上是减函数,在-----文科数学.files/image391.gif) 上是增函数。
上是增函数。
-----文科数学.files/image393.gif)
-----文科数学.files/image395.gif) 在
在-----文科数学.files/image226.gif) 上的最小值是-18,最大值是-6
上的最小值是-18,最大值是-6
(2)-----文科数学.files/image398.gif)
-----文科数学.files/image400.gif)
-----文科数学.files/image402.gif)
当-----文科数学.files/image404.gif) 时,
时,-----文科数学.files/image406.gif) 是增函数,其最小值为
是增函数,其最小值为-----文科数学.files/image408.gif)
-----文科数学.files/image410.gif)
-----文科数学.files/image412.gif) 时也符合题意,
时也符合题意,-----文科数学.files/image414.gif)
22.解:(1)由-----文科数学.files/image241.gif) 知
知-----文科数学.files/image113.gif) 是
是-----文科数学.files/image239.gif) 的中点,
的中点,
设-----文科数学.files/image012.gif) 、
、-----文科数学.files/image014.gif) 两点的坐标分别为
两点的坐标分别为-----文科数学.files/image421.gif)
由-----文科数学.files/image423.gif) 得:
得:-----文科数学.files/image425.gif)
-----文科数学.files/image427.gif)
-----文科数学.files/image429.gif) 点的坐标为
点的坐标为-----文科数学.files/image431.gif)
又-----文科数学.files/image113.gif) 点的直线
点的直线-----文科数学.files/image245.gif) 上:
上:-----文科数学.files/image435.gif)
-----文科数学.files/image437.gif)
-----文科数学.files/image439.gif)
(2)由(1)知-----文科数学.files/image441.gif) ,不妨设椭圆的一个焦点坐标为
,不妨设椭圆的一个焦点坐标为-----文科数学.files/image443.gif) ,设
,设-----文科数学.files/image443.gif) 关于直线
关于直线
-----文科数学.files/image243.gif) 的对称点为
的对称点为-----文科数学.files/image447.gif) ,
,
则有-----文科数学.files/image449.gif) 解得:
解得:-----文科数学.files/image451.gif)
由已知-----文科数学.files/image453.gif) ,
, -----文科数学.files/image455.gif) ,
,
-----文科数学.files/image457.gif) 。
。-----文科数学.files/image274.gif) 所求的椭圆的方程为
所求的椭圆的方程为-----文科数学.files/image460.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com