练习册

  • 练习册
  • 试题
    ∴=又∴∠AOB＝∠DOC∴△AOB-△COD请你判断王颖同学的推理过程是否正确?并说明理由. 【查看更多】

     

    题目列表(包括答案和解析)

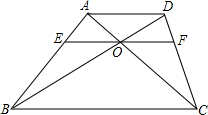    已知：如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，过O点作EF∥A精英家教网D分别交AB，CD于点E，F．
    （1）下面是小明对“△AOB与△DOC是否相似”的解答：
    解：△AOB∽△DOC理由如下：
    ∵AD∥BC（　　）
    ∴△AOD∽△COB
    ∴
    OA
    OC
    =
    OD
    OB
    （　　）
    又∵∠AOB=∠DOC（　　）
    ∴△AOB∽△DOC（　　）
    你认为小明的每一步解答过程是否正确？若正确，请在括号内填上理由；若不正确，请在该步骤后面的括号内打“×”．
    （2）OE与OF有何关系？为什么？
    （3）试求出
    OE
    AD
    +
    OF
    BC
    的值．

    查看答案和解析>>

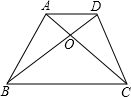    如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，问△AOB与△COD是否相似？有一位同学解答下精英家教网：
    ∵AD∥BC，
    ∴∠ADO=∠CBO，∠DAO=∠BCO．
    ∴△AOD∽△BOC．
    ∴
    AO
    BO
    =
    DO
    CO
    ．
    又∵∠AOB=∠DOC，
    ∴△AOB∽△COD．
    请判断这位同学的解答是否正确并说明理由．

    查看答案和解析>>

    如图：∠AOB∶∠BOC∶∠COD＝2∶3∶4，射线OM、ON分别平分∠AOB与∠COD，又∠MON＝90°，则∠AOB为（    ）

     

    A．20° B．30°         C．40°        D．45°

     

    查看答案和解析>>

    如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，问△AOB与△COD是否相似？有一位同学解答下：
    ∵AD∥BC，
    ∴∠ADO=∠CBO，∠DAO=∠BCO．
    ∴△AOD∽△BOC．
    ∴数学公式．
    又∵∠AOB=∠DOC，
    ∴△AOB∽△COD．
    请判断这位同学的解答是否正确并说明理由．

    查看答案和解析>>

    如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，问△AOB与△COD是否相似？有一位同学解答下
    精英家教网
    ：
    ∵AD∥BC，
    ∴∠ADO=∠CBO，∠DAO=∠BCO．
    ∴△AOD∽△BOC．
    ∴
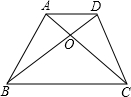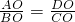    AO
    BO
    =
    DO
    CO
    ．
    又∵∠AOB=∠DOC，
    ∴△AOB∽△COD．
    请判断这位同学的解答是否正确并说明理由．

    查看答案和解析>>


    同步练习册答案