(2013•宜昌)如图1,平面直角坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y
1=ax(x-t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y
2=kx(k为常数,k>0)
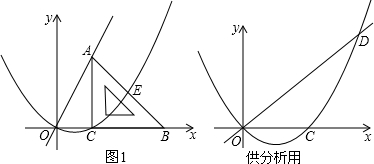
(1)填空:用含t的代数式表示点A的坐标及k的值:A
(t,4)
(t,4)
,k=
;
(2)随着三角板的滑动,当a=
时:
①请你验证:抛物线y
1=ax(x-t)的顶点在函数y=
-x2的图象上;
②当三角板滑至点E为AB的中点时,求t的值;
(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y
2-y
1|的值随x的增大而减小,当x≥t+4时,|y
2-y
1|的值随x的增大而增大,求a与t的关系式及t的取值范围.

