
题目列表(包括答案和解析)
(本小题满分10分)如图,已知抛物线经过A(-2,0),B(-3,3) 及原点 ,顶点为
,顶点为 .
.
(1)求抛物线的解析式;
(2)若点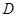 在抛物线上,点
在抛物线上,点 在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3) 是抛物线上第一象限内的动点,过点
是抛物线上第一象限内的动点,过点 作
作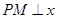 轴,垂足为
轴,垂足为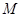 ,是否存在点
,是否存在点 ,使得以
,使得以 、
、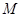 、
、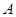 为顶点的三角形与
为顶点的三角形与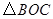 相似?若存在,求出点
相似?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
.(本小题满分12分)
如图,已知在⊙O中,直径AB=10,点E是OA上任意一点,过E作弦CD⊥AB,点F是弧BC上一点,连结AF交CE于H,连结AC、CF、BF。
1.(1)请你找出图中的相似三角形,并对其中的一对相似三角形进行证明;
2.(2)若AE:BE=1:4,求CD长。
3.(3)在(2)的条件下,求![]() 的值。
的值。
(本小题满分10分)如图,已知抛物线经过A(-2,0),B(-3,3) 及原点![]() ,顶点为
,顶点为![]() .
.
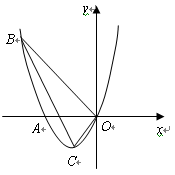
(1)求抛物线的解析式;
(2)若点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)![]() 是抛物线上第一象限内的动点,过点
是抛物线上第一象限内的动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,是否存在点
,是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

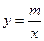 (
( )的图象与一次函数
)的图象与一次函数 的图象交于
的图象交于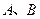 两点,点
两点,点 的坐标为
的坐标为 ,连接
,连接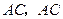 平行于
平行于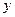 轴.
轴.
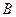 的坐标.
的坐标. 在反比例函数图象上的
在反比例函数图象上的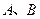 之间的部分滑动(不与
之间的部分滑动(不与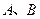 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于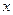 轴、
轴、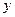 轴,且与线段
轴,且与线段 交于
交于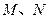 两点,试判断
两点,试判断 点在滑动过程中
点在滑动过程中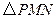 是否与
是否与 总相似,简要说明判断理由.
总相似,简要说明判断理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com