
题目列表(包括答案和解析)
|
及三视图如图所示:(其中M、N分别是AF、BC的中点).
(Ⅰ)求证:MN∥平面CDEF;
(II)求多面体A—CDEF的体积.
(本小题满分12分)一个多面体的直观图和三视图如图所示,其中 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证: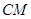
 平面
平面
(2)在线段 上(含
上(含 、
、 端点)确定一点
端点)确定一点 ,使得
,使得
 平面
平面 ,并给出证明;
,并给出证明;
(3)一只小飞虫在几何体 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体 内的概率.
内的概率.


(本小题满分12分)
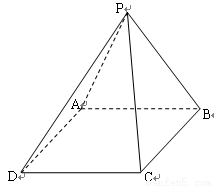
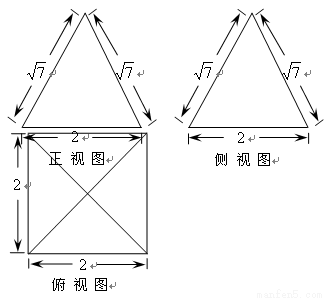
一个多面体的直观图和三视图如图所示:
(I)求证:PA⊥BD;
(II)连接AC、BD交于点O,在线段PD上是否存在一点Q,使直线OQ与平面ABCD所成的角为30o?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分12分)
一个多面体的直观图和三视图如图所示
 (1)求证:
(1)求证: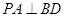 ;(2)是否在线段
;(2)是否在线段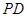 上存在一
上存在一 点,使二面角
点,使二面角 的平
的平
面角为 ,设
,设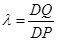 ,若存在,求
,若存在,求 ;若不存在,说明理由
;若不存在,说明理由
 |
|||
 |
|||
(本小题满分12分)
一个多面体的直观图和三视图如图所示
(Ⅰ) 求证: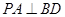 ;
;
(Ⅱ) 若 为
为 上一点,且
上一点,且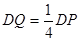 ,求二面角
,求二面角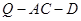 的大小.
的大小.
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
A
B
D
B
C
B
C
D
B
1.提示:.files/image234.gif)
.files/image236.gif) ,故选C。
,故选C。
2.提示:“任意的”否定为“存在”;“>”的否定为“.files/image238.gif) ”,故选A
”,故选A
3.提示:.files/image240.gif) 又
又.files/image242.gif) ,所以
,所以.files/image244.gif) ,故选D。
,故选D。
4.提示:在AB上取点D,使得.files/image246.gif) ,则点P只能在AD内运动,则
,则点P只能在AD内运动,则.files/image248.gif) ,
,
5.提示:排除法选B。
6.提示:由图(1)改为图(2)后每次循环时.files/image250.gif) 的值都为1,因此运行过程出现无限循环,故选D
的值都为1,因此运行过程出现无限循环,故选D
7.提示:由茎叶图的定义,甲得分为7,8,9,15,19,23,24,26,32,41。共11个数,19是中位数,乙得分为5,7,11,11,13,20,22,30,31,40。共11个数,13是中位数。
故选B。
8.提示:.files/image252.gif) 得
得.files/image254.gif) 所以
所以.files/image256.gif) ,故选C。
,故选C。
.files/image257.gif) 9.提示:由
9.提示:由.files/image259.gif) 及
及.files/image261.gif) 得
得
.files/image263.gif) 如图
如图
过A作.files/image265.gif) 于M,则
于M,则
.files/image267.gif)
.files/image269.gif)
.files/image271.gif)
.files/image273.gif) 得
得.files/image275.gif) .
.
故选B.
10.提示:不妨设点(2,0)与曲线.files/image067.gif) 上不同的三的点距离为分别
上不同的三的点距离为分别.files/image277.gif) ,它们组成的等比数列的公比为
,它们组成的等比数列的公比为.files/image279.gif) 若令
若令.files/image281.gif) ,显然
,显然.files/image283.gif) ,又
,又.files/image285.gif) 所以
所以.files/image287.gif) ,
,.files/image289.gif) 不能取到
不能取到.files/image036.gif) 。故选B。
。故选B。
11.提示:使用特值法:取集合.files/image292.gif) 当
当.files/image294.gif) 可以排除A、B;
可以排除A、B;
取集合.files/image296.gif) ,当
,当.files/image298.gif) 可以排除C;故选D;
可以排除C;故选D;
12.提示:n棱柱有.files/image300.gif) 个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)
个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)
.files/image302.gif)
.files/image303.gif)
.files/image304.gif)
.files/image305.gif)
.files/image306.gif)
.files/image307.gif)
2在图4,图6所示的情形,还剩.files/image300.gif) 个顶点;
个顶点;
在图5的情形,还剩.files/image309.gif) 个顶点;
个顶点;
在图2,图3的情形,还剩.files/image311.gif) 个顶点;
个顶点;
在图1的情形,还剩下.files/image313.gif) 个顶点.故选B.
个顶点.故选B. .files/image315.jpg)
二、填空题:
13.4
提示:.files/image317.gif)
.files/image319.gif) 由(1),(2)得
由(1),(2)得.files/image321.gif) 或
或.files/image323.gif) ,所以
,所以.files/image325.gif) 。
。
14..files/image327.gif)
提示:斜率.files/image329.gif) ,切点
,切点.files/image331.gif) ,所以切线方程为:
,所以切线方程为:.files/image333.gif)
15..files/image335.gif)
提示:当.files/image337.gif) 时,不等式无解,当
时,不等式无解,当.files/image339.gif) 时,不等式变为
时,不等式变为.files/image341.gif) ,
,
由题意得.files/image343.gif) 或
或.files/image345.gif) ,所以,
,所以,.files/image347.gif) 或
或.files/image349.gif)
16..files/image351.gif)
三、解答题:
17.解:① ∵.files/image353.gif) ∴
∴.files/image355.gif) 的定义域为R;
的定义域为R;
② ∵.files/image357.gif) ,
,
∴.files/image178.gif) 为偶函数;
为偶函数;
③ ∵.files/image360.gif) , ∴
, ∴.files/image178.gif) 是周期为
是周期为.files/image363.gif) 的周期函数;
的周期函数;
④ 当.files/image365.gif) 时,
时,.files/image178.gif) =
=.files/image367.gif) ,
,
∴当.files/image365.gif) 时
时.files/image178.gif) 单调递减;当
单调递减;当.files/image371.gif) 时,
时,
.files/image178.gif) =
=.files/image373.gif) ,
,
.files/image178.gif) 单调递增;又∵
单调递增;又∵.files/image178.gif) 是周期为
是周期为.files/image363.gif) 的偶函数,∴
的偶函数,∴.files/image178.gif) 在
在.files/image378.gif) 上单调递增,在
上单调递增,在.files/image380.gif) 上单调递减(
上单调递减(.files/image382.gif) );
);
⑤ ∵当.files/image384.gif) 时
时.files/image386.gif) ;
;
当.files/image387.gif) 时
时.files/image389.gif) .∴
.∴.files/image178.gif) 的值域为
的值域为.files/image392.gif) ;
;
⑥由以上性质可得:.files/image178.gif) 在
在.files/image395.gif) 上的图象如图所示:
上的图象如图所示:
.files/image397.jpg)
18.解:(Ⅰ)取PC的中点G,连结EG,GD,则.files/image399.gif)
由(Ⅰ)知FD⊥平面PDC,.files/image401.gif) 面PDC,所以FD⊥DG。
面PDC,所以FD⊥DG。
所以四边形FEGD为矩形,因为G为等腰Rt△RPD斜边PC的中点,
所以DG⊥PC,
|