(本小题满分8分)

   某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠围墙(墙的长度不限)，另三边用木栏围成，建成的苗圃为如图所示的长方形ABCD。已知木栏总长为120米，设AB边的长为x米，长方形ABCD的面积为S平方米．

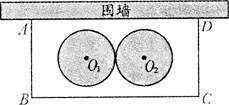
   1.(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)．当x为何值时，S取得最值(请指出是最大值还是最小值)?并求出这个最值；

   2.(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆，其圆心分别为和，且到AB、BC、AD的距离与到CD、BC、AD的距离都相等，并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面，以方便同学们参观学习．当(l)中S取得最值时，请问这个设计是否可行?若可行，求出圆的半径；若不可行，清说明理由．

(本小题满分12分)

   如图，在平面直角坐标系中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知，，△ABC的面积，抛物线

经过A、B、C三点。

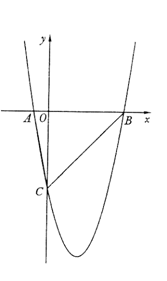
   1.(1)求此抛物线的函数表达式；

   2.(2)设E是y轴右侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；

   3.(3)在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为？若存在，求出点M的坐标；若不存在，请说明理由．

(本小题满分10分)在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为(0°＜＜180°)，得到△A₁B₁C．

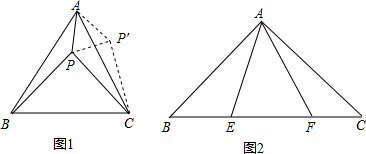
(1)如图1，当AB∥CB₁时，设A₁B₁与BC相交于点D．证明：△A₁CD是等边三角形；

(2)如图2，连接AA₁、BB₁，设△ACA₁和△BCB₁的面积分别为S₁、S₂．

求证：S₁∶S₂＝1∶3；

(3)如图3，设AC的中点为E，A₁B₁的中点为P，AC＝a，连接EP．当等于多少度时，EP的长度最大，最大值是多少？