
题目列表(包括答案和解析)


 如图所示,在某海岛上的观察所A发现海上某船只B并测得其俯角α=8°14′,已知观察所A的标高(当水位为0m时的高度)为43.74m,当时水位为+2.63m,求观察所A到船只B的水平距离BC.(精确到1m)
如图所示,在某海岛上的观察所A发现海上某船只B并测得其俯角α=8°14′,已知观察所A的标高(当水位为0m时的高度)为43.74m,当时水位为+2.63m,求观察所A到船只B的水平距离BC.(精确到1m)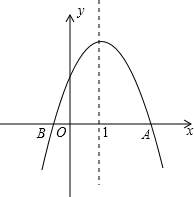 (1997•重庆)如图,已知二次函数y=ax2-bx-c的图象与x轴交于A、B两点,当时x=1,二次函数取得最大值4,且|OA|=-
(1997•重庆)如图,已知二次函数y=ax2-bx-c的图象与x轴交于A、B两点,当时x=1,二次函数取得最大值4,且|OA|=-| 1 | n |

| 1 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com