
题目列表(包括答案和解析)
(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
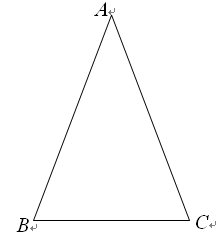
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad ![]() 的值为( )A.
的值为( )A. ![]() B.1 C.
B.1 C. ![]() D.2
D.2
(2)对于![]() ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知![]() ,其中
,其中![]() 为锐角,试求sad
为锐角,试求sad 的值.
的值.
(本小题满分9分)已知A、B两地的路程为240千米,某经销商每天都要用汽
车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和
火车中的一种进行运输,且须提前预订.。现在有货运收费项目及收费标准表,行驶路程S
(千米)与行驶时间t(时)的函数图象(如图13中①),上周货运量折线统计图(如图13
中②)等信息如下:
(1)汽车的速度为__________千米/时,火车的速度为_________千米/时;
(2)设每天用汽车和火车运输的总费用分别为y汽(元)和y火(元),分别求y汽、y火与x的函数关系式(不必写出x的取值范围)及x为何值时y汽>y火;(总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前下周预定哪种运输工具,才能使每天的运输总费用较省?
(本小题满分9分)已知A、B两地的路程为240千米,某经销商每天都要用汽
车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和
火车中的一种进行运输,且须提前预订.。现在有货运收费项目及收费标准表,行驶路程S
(千米)与行驶时间t(时)的函数图象(如图13中①),上周货运量折线统计图(如图13
中②)等信息如下:
(1)汽车的速度为__________千米/时,火车的速度为_________千米/时;
(2)设每天用汽车和火车运输的总费用分别为y汽(元)和y火(元),分别求y汽、y火与x的函数关系式(不必写出x的取值范围)及x为何值时y汽>y火;(总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前下周预定哪种运输工具,才能使每天的运输总费用较省?
(本小题满分12分)已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.
1.(1)填空:菱形ABCD的边长是 ▲ 、面积是
▲ 、 高BE的长是 ▲ ;
2.(2)探究下列问题:
①若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式,以及S的最大值;
②若点P的速度为每秒1个单位,点Q的速度变为每秒k个单位,在运动过程中,任何时刻都有相应的k值,使得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形.请探究当t = 4 秒时的情形,并求出k的值.
(本小题满分5分)某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级,现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
1. (1)共抽测了多少人?
2. (2)样本中B等级的频率是多少?
3.(3) 如果要绘制扇形统计图,A等级在扇形统计图中所占的圆心角是多少度?
4.(4)该校九年级的毕业生共300人,假如“综合素质”等级为A或B的学生才能报考示范性高中,请你计算该校大约有多少名学生可以报考示范性高中?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com