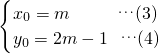阅读材料:当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x
2-2mx+m
2+2m-1…(1)
得:y=(x-m)
2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x
0,y
0),则:
当m的值变化时,顶点横、纵坐标x
0,y
0的值也随之变化,将(3)代入(4)
得:y
0=2x
0-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是
,其中运用的公式是
.由(3)、(4)得到(5)所用的数学方法是
.
②根据阅读材料提供的方法,确定抛物线y=x
2-2mx+2m
2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x
2-2mx+2m
2-4m+3与x轴两交点A(x
1,0)、B(x
2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x
1-x
2|
2=(x
1+x
2)
2-4x
1x
2).