
题目列表(包括答案和解析)
(本题满分12分)
已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.
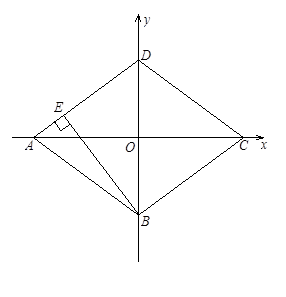
1.(1)填空:菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ;
2.(2)探究下列问题:
若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时
② △APQ的面积S关于t的函数关系式,以及S的最大值;
3.(3)在运动过程中是否存在某一时刻使得△APQ为等腰三角形,若存在求出t的值;若不存在说明理由.
(本题满分12分)在直角坐标系中,抛物线![]() 经过点(0,10)
经过点(0,10)
和点(4,2).

1.(1) 求这条抛物线的函数关系式.
2.(2)如图,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线![]() 滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,AB正好落在x轴上.
滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,AB正好落在x轴上.
①求边BC的长.
②当矩形ABCD在滑动过程中被x轴分成两部分的面
积比为1:4时,求点C的坐标.
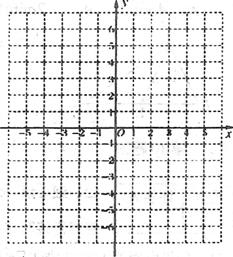
(本题满分l0分)在如下图所示的平面直角坐标系中画出下面各点:A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);并解答下列各题
(1)A点到原点O的距离是________________________。
(2)将点C沿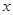 轴的负方向平移6个单位,它与点_______________重合。
轴的负方向平移6个单位,它与点_______________重合。
(3)连接CE,则直线CE与Y轴是什么关系?
(4)点F分别到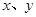 轴的距离是多少?
轴的距离是多少?
(本题满分12分)我们设想用电脑模拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
(1)希望A球撞击桌边上C点后反弹,再击中B球,请给出一个算法,告知电脑怎样找到点C,并求出C点的坐标。
(2)设桌边RQ上有一球袋S(100,120),判定6号球B被从C点反弹出的白球撞击后能否直接落入球袋S中,(假定6号球被撞后速度足够大)。
(3)若用白球A直接击打6号球B,使6号球B撞击桌边OP上的D点后反弹,问6号球B从D点反弹后能否直接进入球袋Q中?(假定6号球被撞后速度足够大)
(本题满分12分,每小题满分各4分)已知平面直角坐标系xOy(如图1),一次函数![]() 的图 像与y轴交于点A,点M在正比例函数
的图 像与y轴交于点A,点M在正比例函数![]() 的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
(1)求线段AM的长;
(2)求这个二次函数的解析式;
(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数的图像上,点D在一次函数![]() 的图像上,且四边形ABCD是菱形,求点C的坐标.
的图像上,且四边形ABCD是菱形,求点C的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com