
题目列表(包括答案和解析)
(本题满分12分)
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在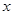 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为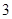 ,最小值为
,最小值为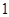 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线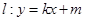 与椭圆
与椭圆 相交于
相交于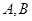 两点(
两点(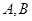 不是左右顶点),且以
不是左右顶点),且以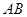 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点.求证:直线
的右顶点.求证:直线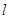 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
(本题满分12分)
已知椭圆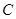 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆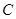 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为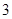 ,最小值为
,最小值为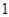 .
.
(1)求椭圆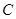 的标准方程;
的标准方程;
(2)若直线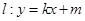 与椭圆
与椭圆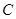 相交于
相交于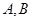 两点(
两点(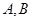 不是左右顶点),且以
不是左右顶点),且以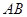 为直径的圆过椭圆
为直径的圆过椭圆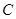 的右顶点.求证:直线
的右顶点.求证:直线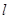 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
(本题满分12分)
已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,左右焦点分别为
轴上,左右焦点分别为![]() ,且
,且![]() ,点
,点![]() )在椭圆
)在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且△
两点,且△![]() 的面积
的面积![]() ,求以
,求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
(本题满分12分)
已知椭圆![]() 的焦点在
的焦点在![]() 轴上,中心在原点,离心率
轴上,中心在原点,离心率![]() ,直线
,直线![]() 和以原点为圆心,椭圆
和以原点为圆心,椭圆![]() 的短半轴为半径的圆
的短半轴为半径的圆![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,点
,点![]() 是椭圆上异于
是椭圆上异于![]() 、
、![]() 的任意一点,设直线
的任意一点,设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() 为定值;
为定值;
(Ⅲ)设椭圆方程![]() ,
,![]() 、
、![]() 为长轴两个端点,
为长轴两个端点, ![]() 为椭圆上异于
为椭圆上异于![]() 、
、![]() 的点,
的点, ![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 的斜率,利用上面(Ⅱ)的结论得
的斜率,利用上面(Ⅱ)的结论得![]() ( )(只需直接写出结果即可,不必写出推理过程).
( )(只需直接写出结果即可,不必写出推理过程).
 (本题满分12分)已知椭圆E:
(本题满分12分)已知椭圆E:![]() (其中
(其中![]() ),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线
),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线![]() 分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
(Ⅰ)若直线L在![]() 轴上的截距为
轴上的截距为![]() ,求证: 直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若
,求证: 直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若![]() 的最大值为1200,求椭圆E的方程.
的最大值为1200,求椭圆E的方程.
一.选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
B
A
C
D
D
D
A
B
A
A
二.填空题
13.4; 14.  ; 15.15; 16.
; 15.15; 16. ,
, 可以填写任一实数.
可以填写任一实数.
三.解答题
17. (Ⅰ)列表:


2
6
10
14

0





1
3
1

1
描点作图,得图象如下.
 6分
6分
(Ⅱ)

所以,当 ,即
,即 时,函数
时,函数 取得最小值
取得最小值 . 12分
. 12分
18.由图可知,参加活动1次、2次和3次的学生人数分别为5、25和20.
(I)该班学生参加活动的人均次数为 =
= . 6分
. 6分
(II)从该班中任选两名学生,他们参加活动次数恰好相等的概率为 .
12分
.
12分
19.(Ⅰ)∵AD=2AB=2,E是AD的中点,
∴△BAE,△CDDE是等腰直角三角形,
易知,∠BEC=90°,即BE⊥EC
又∵平面D′EC⊥平面BEC,面D′EC∩面BEC=EC,
∴BE⊥面D′EC,又CD′ 面D′EC,∴BE⊥CD′.
6分
面D′EC,∴BE⊥CD′.
6分
(Ⅱ)法一:设M是线段EC的中点,过M作MF⊥BC
垂足为F,连接D′M,D′F,则D′M⊥EC
∵平面D′EC⊥平面BEC,
 ∴D′M⊥平面EBC,
∴D′M⊥平面EBC,
∴MF是D′F在平面BEC上的射影,
由三垂线定理得:D′F⊥BC
∴∠D′FM是二面D′―BC―E的平面角.
在Rt△D′MF中,
∴ ,
,
即二面角D′―BC―E的正切值为 .
12分
.
12分
法二:如图,以EB,EC为x轴,y轴,过E垂直于平面BEC的射线为z轴,建立空间直角坐标系,
则
设平面BEC的法向量为 ;平面D′BC的法向量为
;平面D′BC的法向量为


由
取
∴

∴二面角D′―BC―E的正切值为 .
12分
.
12分
20.(I) ,
,

(II) 由(I)知
由(I)知


21(Ⅰ)设椭圆C的方程为 ,则由题意知b = 1.
,则由题意知b = 1.

∴椭圆C的方程为
 …………………………………………………6分
…………………………………………………6分
(Ⅱ)易知直线 的斜率为
的斜率为 ,从而直线
,从而直线 的斜率为1.设直线的方程为
的斜率为1.设直线的方程为 ,代如椭圆的方程,并整理可得
,代如椭圆的方程,并整理可得 .设
.设 ,则
,则 ,
, .于是
.于是


解之得 或
或 .
.
当 时,点
时,点 即为直线
即为直线 与椭圆的交点,不合题意.当
与椭圆的交点,不合题意.当 时,经检验知
时,经检验知 和椭圆相交,符合题意.
和椭圆相交,符合题意.
所以,当且仅当直线 的方程为
的方程为 时, 点
时, 点 是
是 的垂心. 12分
的垂心. 12分
22.(Ⅰ)对一切 有
有

于是, 

 (
( ) 5分
) 5分
(Ⅱ)由 及
及
两式相减,得: 


∴ . 10分
. 10分
(Ⅲ) 由于 ,
,
所以, 14分
14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com