练习册

  • 练习册
  • 试题
    10．如图:是3×3的一个正方形.图中每一个小方格都是完全相同的正方形.现从图中的16个顶点中任选三个顶点构成三角形.则其中直角三角形的个数为 A．160 B．200 C．240 D．260 第Ⅱ卷 【查看更多】

     

    题目列表(包括答案和解析)

    如图：是3×3的一个正方形，图中每一个小方格都是完全相同的正方形，现从图中的16个顶点中任选三个顶点构成三角形，则其中直角三角形(如△ABC，△DBC)的个数为

    [　　]

    A．160

    B．200

    C．240

    D．260

    查看答案和解析>>

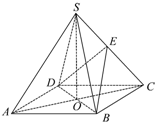    如图，在四棱锥SABCD中，底面ABCD是正方形，四个侧面都是等边三角形，AC与BD交于点O，E为侧棱SC上的一点．
    （1）若E为SC的中点，求证：SA∥平面BDE；
    （2）求证：平面BDE⊥平面SAC；
    （3）若正方形ABCD边长为2，求四棱锥SABCD的体积．

    查看答案和解析>>

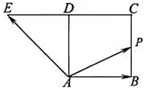    精英家教网如图1在透明塑料做成的长方体容器中灌进一些水，固定容器的一边将其倾倒，随着容器的倾斜度不同，水的各个表面的图形的形状和大小也不同．某个同学找出这些图形的形状和大小之间所存在的一些“规律”：①有水的部分始终呈棱柱形；②没有水的部分始终呈棱柱形；③水面面积的大小是变化的，如图2所示，倾斜度越大（即α越小），水面的面积越大．④如果长方体的倾斜角为α，则水面与容器底面所成的角为90°-α．
    其中对“规律”的叙述正确的个数有（　　）
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    精英家教网如图，四边形ABCD是边长为1的正方形，延长CD至E，使得DE=CD．动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，
    AP
    =λ
    AB
    +μ
    AE
    ．
    下列三个命题：
    ①当点P与D重合时，λ+μ=2；
    ②λ+μ的最小值为0，λ+μ的最大值为3；
    ③在满足1≤λ+μ≤2的动点P中任取两个不同的点P1和P2，则0＜|
    P1P2
    |≤
    1
    2
    或1≤|
    P1P2
    |≤
    		2
    ．
    其中正确命题的个数为（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    如图是一几何体的平面展开图，其中ABCD为正方形，E、F

    分别为PA、PD的中点。在此几何体中，给出下面四个结论：

    （1）直线BE 与直线CF异面；     （2）直线BE与直线AF异面

    （3）直线EF//平面PBC            （4）平面BCE平面PAD

    其中正确的有：

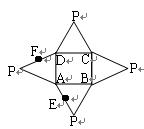
    A 、（2）（3）       B、（1）(2)     C、（2）（4）    D、（1）（4）

    查看答案和解析>>

     

    一、选择题

    BBACA   DCBBB（分类分布求解）

    二、填空题

    11．{2，7}     12．840    13．1    14．2    15．（圆锥曲线定义）

    16．解：（1）由

       （2）由余弦定理知：

        又

    17．解：设事件A为“小张被甲单位录取”，B为“被乙单位录取”，C为“被丙单位录取”。

       （1）小张没有被录取的概率为：

       （2）小张被一个单位录取的概率为

        被两个单位同时录取的概率为

        被三个单位录取的概率为：所以分布列为：

    ξ

    0

    1

    2

    3

    P

        所以：

    18．解：（1）

       

        所以：

    19．解：（1）连接B1D1，ABCD―A1B1C1D1为四棱柱，

    ，

    则在四边形BB1D1D中（如图），

    得△D1O1B1≌△B1BO，可得∠D1O1B1=∠OBB1=90°，

    即D1O1⊥B1O

       （2）连接OD1，显然：∠D1OB1为所求的角，

    容易计算：∠D1OB1

        所以：

    20．解：（1）曲线C的方程为

       （2）当直线的斜率不存在时，它与曲线C只有一个交点，不合题意，

        当直线m与x轴不垂直时，设直线m的方程为

       代入    ①

        恒成立，

        设交点A，B的坐标分别为

    ∴直线m与曲线C恒有两个不同交点。

    则    ②        ③

     

           当k=0时，方程①的解为

       

           当k=0时，方程①的解为

        综上，由

    21．解：（1）当

        由

    0

    递增

    极大值

    递减

        所以

       （2）

           ①

        由得

            ②

        由①②得：即得：

        与假设矛盾，所以成立

       （3）解法1：由（2）得：

       

        由（2）得：

    解法3：可用数学归纳法：步骤同解法2

    解法4：可考虑用不等式步骤略

     


    同步练习册答案