
题目列表(包括答案和解析)
已知直线MN与双曲线C: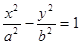 的左右两支分别交于M,N两点,与双曲线C的右准线相交于P点,点F为右焦点,若
的左右两支分别交于M,N两点,与双曲线C的右准线相交于P点,点F为右焦点,若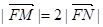 ,
,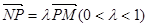 ,则实数
,则实数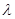 的值为 .
的值为 .
已知直线MN与双曲线C: 的左右两支分别交于M,N两点,与双曲线C的右准线相交于P点,点F为右焦点,若
的左右两支分别交于M,N两点,与双曲线C的右准线相交于P点,点F为右焦点,若 ,
, ,则实数
,则实数 的值为 .
的值为 .
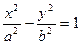 的左右两支分别交于M,N两点,与双曲线C的右准线相交于P点,点F为右焦点,若
的左右两支分别交于M,N两点,与双曲线C的右准线相交于P点,点F为右焦点,若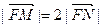 ,
,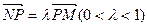 ,则实数
,则实数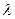 的值为 .
的值为 .已知椭圆![]() :
:![]() 与双曲线
与双曲线![]() 有公共焦点,且离心率为
有公共焦点,且离心率为![]() .A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:
.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x轴上方的动点.直线AS,BS分别与直线l:![]() 分别交于M,N两点.
分别交于M,N两点.
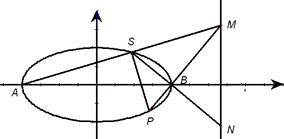
(1)求椭圆C的方程;
(2)延长MB交椭圆C于点P,若PS⊥AM,试证明MS2=MB·MP.
(3)当线段MN的长度最小时,在椭圆C上是否存在点T,使得△TSB的面积为![]() ?若存在确定点T的个数,若不存在,说明理由.
?若存在确定点T的个数,若不存在,说明理由.
| y2 | 3 |
一、选择题
BBACA DCBBB(分类分布求解)
二、填空题
11.{2,7} 12.840 13.1 14.2 15.--理科数学.files/image014.gif) (圆锥曲线定义)
(圆锥曲线定义)
16.解:(1)由--理科数学.files/image110.gif)
(2)由余弦定理知:--理科数学.files/image112.gif)
又--理科数学.files/image114.gif)
17.解:设事件A为“小张被甲单位录取”,B为“被乙单位录取”,C为“被丙单位录取”。
(1)小张没有被录取的概率为:--理科数学.files/image116.gif)
(2)小张被一个单位录取的概率为--理科数学.files/image118.gif)
被两个单位同时录取的概率为--理科数学.files/image120.gif)
被三个单位录取的概率为:--理科数学.files/image122.gif) 所以分布列为:
所以分布列为:
ξ
0
1
2
3
P
--理科数学.files/image124.gif)
--理科数学.files/image126.gif)
--理科数学.files/image128.gif)
--理科数学.files/image130.gif)
所以:--理科数学.files/image132.gif)
18.解:(1)--理科数学.files/image134.gif)
--理科数学.files/image136.gif)
|