题目列表(包括答案和解析)
、
、
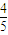（允许小张被多个单位同时录用）．大学毕业的小张到甲、乙、丙三个单位应聘，各单位是否录用他相互独立，其被录用的概率分别为
、
、
(允许小张被多个单位同时录用)．
(1)小张没有被录用的概率；
(2)求小张被2个单位同时录用的概率；
(3)设没有录用小张的单位个数为ξ，求ξ的分布列和它的数学期望．
大学毕业生小张到甲、乙、丙三个单位应聘，各单位是否录用他是相互独立的，其被录用的概率分别为
，
，
（允许小张被多个单位同时录用)，
(1)求小张没有被录用的概率；
(2)求小张恰被两个单位录用的概率。
、
、
、
.(允许小张被多个单位同时录用)(1)求小张没有被录用的概率;
(2)求小张恰被三个单位录用的概率;
(理)(3)设录用小张的单位个数为ξ,求ξ的分布列和它的数学期望.
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
一、选择题
BBACA DCBBB（分类分布求解）
二、填空题
11．{2，7} 12．840 13．1 14．2 15．
（圆锥曲线定义）
16．解：（1）由
（2）由余弦定理知：
又
17．解：设事件A为“小张被甲单位录取”，B为“被乙单位录取”，C为“被丙单位录取”。
（1）小张没有被录取的概率为：
（2）小张被一个单位录取的概率为
被两个单位同时录取的概率为
被三个单位录取的概率为：
所以分布列为：
ξ
0
1
2
3
P
所以：
18．解：（1）
|
，
的斜率不存在时，它与曲线C只有一个交点，不合题意，
①
恒成立， 
② 
③
当k=0时，方程①的解为
当k=0时，方程①的解为
①
得
②
即得：
与假设矛盾，所以成立
解法3：可用数学归纳法：步骤同解法2
步骤略