
题目列表(包括答案和解析)
(1)甲乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴Ox表示这条公路,原点O为零千米路标(如图1),并作如下约定:
①速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止.
②汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;汽车位置在数轴上的坐标s<0,表示汽车位于零千米路标的左侧;汽车位置在数轴上的坐标s=0,表示汽车恰好位于零千米路标处.
遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图象的形式画在了同一直角坐标系中,如图2,请解答下列问题:
①就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格.
| 行驶方向 | 速度的大小(km/h) | 出发前的位置 | |
| 甲车 | |||
| 乙车 |
②甲乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,请说明理由.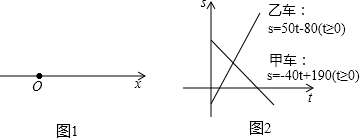
(2)在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余的高度y(cm)与燃烧时间x(分钟)的关系如下图所示,根据图象提供的信息解答下列问题:
①指出两根蜡烛燃烧前的高度;
②分别求出甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
③x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等.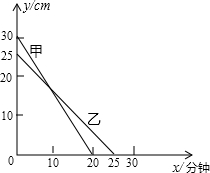
| (1)甲乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴O表示这条公路,原点O为零千米路标(如图1),并作如下约定: ①速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止。 ②汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;汽车位置在数轴上的坐标s<0,表示汽车位于零千米路标的左侧;汽车位置在数轴上的坐标s=0,表示汽车恰好位于零千米路标处,遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图象的形式画在了同一直角坐标系中,如图2。 | ||||||||||||
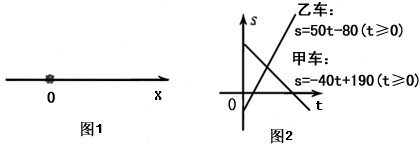 | ||||||||||||
| 请解答下列问题: ①就这两个一次函数图像所反映的两汽车在这条公路上行驶的状况填写如下的表格: | ||||||||||||
| ||||||||||||
| (2)在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余的高度y(cm)与燃烧时间x(分钟)的关系如下图所示,根据图像提供的信息解答下列问题: | ||||||||||||
 | ||||||||||||
| ①指出两根蜡烛燃烧前的高度; ②分别求出甲、乙两根蜡烛燃烧时y与x之间的函数关系式; ③x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等。 |
某校九年级一班数学科代表对本班期末考试数学成绩(成绩去整数,满分为100分)作了统计分析,绘制成如下频数、频率统计表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
| 分组 | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
(1)在频数、频率统计表中a=______;b=______;并将频数分布直方图补充完整.
(2)若该校九年级共有12个班,每班人数相同,成绩在79.5以上的为A级,请你估算在此次考试中,全年级学生数学成绩为A级的人数为多少人?
(3)若在本班49.5~59.5和89.5~100.5两个分数段任选两名同学,求这两名同学成绩之差的绝对值不大于10分的概率是多少?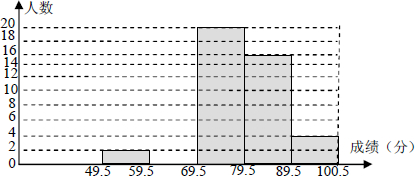


据悉,某市发改委拟于今年4月27日举行居民用水价格调整听证会,届时将有两个方案提供听证。如图(1),射线OA、射线OB分别表示现行的、方案一的每户每月的用水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;方案二如图(2)表格所示,每月的每立方米用水价格由该月的用水量决定,且第一、二、三级的用水价格之比为1︰1.5︰2(精确到0.01元后).
【小题1】写出现行的用水价是每立方米多少元?
【小题2】求图(1)中m的值和射线OB所对应的函数解析式,并写出定义域;
【小题3】若小明家某月的用水量是a立方米,请分别写出三种情况下(现行的、方案一和方案二)该月的水费b(用a的代数式表示);
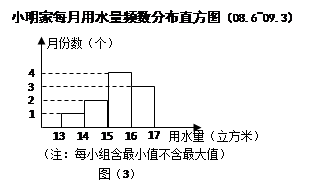
【小题4】小明家最近10个月来的每月用水量的频数分布直方图
如图(3)所示,估计小明会赞同采用哪个方案?请说明理由。 


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com