已知数列{a_n}满足以下两个条件：①点（a_n，a_n+1）在直线y=x+2上，②首项a₁是方程3x²-4x+1=0的整数解，
（I）求数列{a_n}的通项公式；
（II）数列{a_n}的前n项和为S_n，等比数列{b_n}中，b₁=a₁，b₂=a₂，数列{b_n}的前n项和为T_n，解不等式T_n≤S_n．

解方程:(1+i)z=3-i.

给出问题：已知满足，试判定的形状.某学生的解答如下：

解：（i）由余弦定理可得，

，

，

,

故是直角三角形.

（ii）设外接圆半径为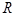.由正弦定理可得，原式等价于

，

故是等腰三角形.

综上可知，是等腰直角三角形.

请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果.　　    　　　　　.

 

（本小题满分14分）为研究我校高二年级的男生身高，随机抽取40名男生，实测身高数据（单位：厘米）如下：

171      173    163    169    166    167    168.5  160    170    165

175      169    167    156    165.5 168    170    184    168    174

165      170    174    161    177     175.5  173    164    175    171.5

176      159    172    181    175.5  165    163    173    170.5  171

（I）依据题目提示作出频率分布表；

（Ⅱ）在（I）的条件下画出频率分布直方图并且画出其频率分布折线图；

（Ⅲ）试利用频率分布的直方图估计样本的平均数。

【解】（I）最低身高156cm，最高身高184cm，确定组距为4，作频率分布表如下：

身高（cm）	频数累计	频数	频率（％）

 

 

（Ⅱ）频率直方图如下：